Течения в трубе. Формула Пуазейля

Число задач, для которых получено аналитическое решение гидродинамической системы уравнений для модели вязкой жидкости, немногочисленно. Рассмотрим одну из них, в которой определяются параметры установившегося прямолинейного потока вязкой несжимаемой жидкости в круглой трубе. Эта задача имеет важное прикладное значение, поскольку транспортировка жидкости (воды, нефти и т.д.) и газа осуществляется по трубопроводам. Во многих случаях инженерные расчеты напорных течений вязкой жидкости в трубопроводах приходится осуществлять, принимая ряд существенных упрощений, которых нет в реальных течениях. Однако полученные решения оказываются вполне удовлетворительными для практических потребностей.

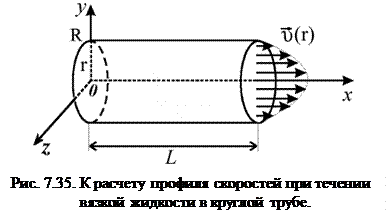
Поставим задачу следующим образом. По заданным начальным и граничным условиям для потока в трубе требуется вычислить распределение скорости по сечению трубы и определить объемный расход жидкости. Систему координат для потока в круглой трубе радиуса 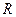и длины 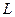выберем так, как показано на рис. 7.35. Из уравнения неразрывности при условии стационарности течения имеем

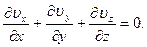(7.76)

Считаем, что течение плоское со скоростью, направленной вдоль оси 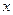, тогда

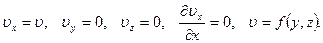(7.77)

Векторное уравнение Навье – Стокса для стационарного движения вязкой жидкости имеет вид

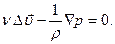
С учетом (7.77) в компонентной форме его можно записать так:

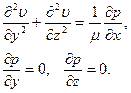(7.78)

Так как давление 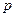не зависит от координаты 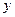, то левая и правая части уравнения Навье – Стокса взаимно независимы. Следовательно, если правая часть уравнения зависит от переменной 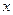, то левую часть можно считать зависящей только от переменной 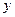. Обозначим правую часть уравнения следующим образом:

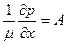. (7.79)

Перейдем к записи уравнений в цилиндрической системе координат :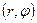

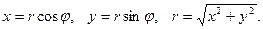
В результате уравнение движения вязкой жидкости в трубе примет такой вид:

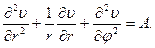(7.80)

Поток в трубе осесимметричен, поэтому в (7.80) производные по углу 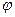можно опустить:

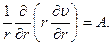
После преобразования имеем

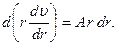
Группируем производные под знак дифференциала:

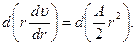
Интегрируем с точностью до константы:

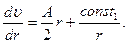
После второго интегрирования получаем

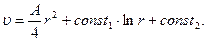(7.81)

Для определения констант интегрирования используем следующие граничные условия. Полагаем, что на оси трубы при 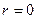скорость достигает максимального значения 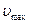, а на стенке трубы при 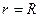из-за прилипания скорость обращается в нуль. Тогда для постоянных интегрирования получаем: , .

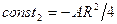Градиент давления в (7.79) можно представить в виде отношения перепада давления 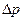к длине трубы :

.

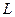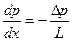Тогда для зависимости скорости от радиальной координаты получаем следующую формулу:

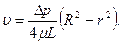(7.82)

Формула (7.82) для распределения скорости по радиусу в круглой трубе называется законом Пуазейля. Впервые эта формула была получена опытным путем французским врачом Ж. Пуазейлем (1799 – 1869), исследовавшим движение крови в сосудах животных.

По известным компонентам вектора скорости 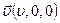можно легко вычислить компоненты тензора скоростей деформаций

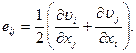
В нашем случае, очевидно,

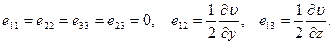
Зная компоненты тензора скоростей деформаций, на основе закона Навье – Стокса

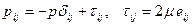
легко вычислить компоненты тензора напряжений:

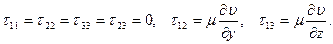
Отсюда ясно, что 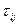не зависят от 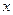и что компоненты тензора вязких напряжени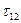й и 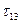вызваны градиентом скорости .

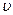Нетрудно убедиться, что рассматриваемое движение жидкости вихревое, несмотря на то, что линии тока являются прямыми. Вектор вихря 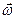в нашем случае можно вычислить по формуле

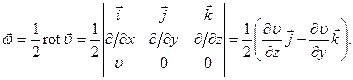
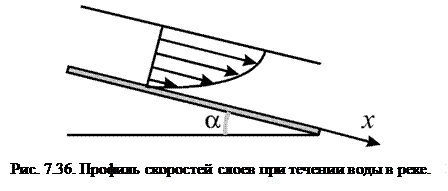
Для течения Пуазейля, как следует из (7.82), скорость потока в трубе в поперечном направлении изменяется по параболе. Параболический профиль скорости слоев будет и при течении жидкости между двумя пластинами, как изображено на рис. 7.26. Если этот рисунок разрезать посередине на высоте 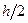и наклонить нижнюю пластину под углом 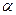к горизонту, то получится картина течения воды в реке под действием силы тяжести (см. рис. 7.36). При расчете профиля скоростей течения вместо градиента давления можно использовать компоненту силы тяжести .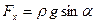

Из закона Пуазейля следует, что при 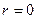(на оси трубы), скорость достигает максимального значения, которое равно

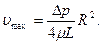(7.83)

Для средней скорости получаем

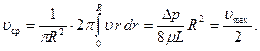(7.84)

Объемный расход 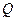потока вязкой жидкости в круглой трубе вычисляется следующим образом:

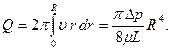(7.85)

Это уравнение Хагена – Пуазейля играет значительную роль в физиологии нашего кровообращения. Капиллярная система человека имеет длину 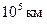(около 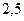окружности Земли!). Повышение мускульной деятельности требует увеличения тока крови 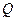. Это наиболее действенно достигается расширением капилляров 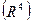. Расширенная сеть сосудов должна быть наполнена. Требуемое количество крови заимствуется, прежде всего, из селезенки и печени.

Точные решения уравнений Навье – Стокса получены также для описания течений жидкостей, обладающих относительно большой вязкостью. Этот результат связывают с Н.Н. Петровым (1836 – 1920), который разработал гидродинамическую теорию смазки. В его теории обоснована способность тел, смазанных сильно вязкими жидкостями по контактной поверхности, воспринимать значительные нагрузки при незначительном трении с толщиной смазочного слоя, измеряемой сотыми долями миллиметра.

Вычислим силу 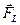, действующую со стороны жидкости на участок длины 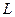трубы круглого поперечного сечения. С одной стороны, из уравнения количества движения для жидкого цилиндра радиуса 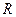и длины 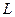будем иметь

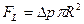. (7.86)

С другой стороны, касательное напряжение, действующее со стороны жидкости на стенку, можно вычислить по закону Навье – Стокса

,

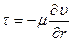откуда по (7.82) при 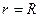будем иметь

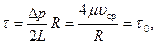(7.86’)

т.е. касательное напряжение на стенках трубы постоянно, и сила сопротивления 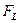будет равна

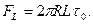(7.87)

Движение жидкости сопровождается взаимодействием со средой, являющейся внешней по отношению к течению, и одновременно внутренним трением между частицами потока. Гидравлическое сопротивление делится на две группы: сопротивление по длине и сопротивление местное, возникающее при взаимодействии жидкости с различными препятствиями на пути потока (например, задвижками, кранами, решетками и т.д.).

Коэффициентом трения 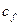называется отношение силы 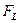к скоростному напору 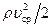и к некоторой характерной площади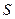

Если за 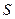принять площадь участка боковой поверхности трубы, на которую рассчитывается сопротивление, то в случае круглой трубы для 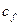по (7.86) и (7.87) получим

,

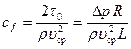или, на основе (7.84), придем к формуле

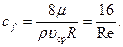(7.88)

Зависимость коэффициента гидравлического сопротивления от числа Рейнольдса для потоков в трубах, соответствующая равенству (7.88), как показывает опыт, хорошо оправдывается для ламинарных течений. Для турбулентного режима течения в трубах зависимость коэффициента гидравлического сопротивления от числа Рейнольдса будет иной.