Идеальной несжимаемой жидкости

Задача о движении сферы в безграничном объеме

Рассмотрим задачу о движении абсолютно твердой сферы в безграничной массе идеальной несжимаемой жидкости, когда на жидкость не действуют внешние массовые силы.

Пусть сфера радиуса 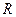движется поступательно относительно некоторой неподвижной системы отсчета 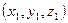со скоростью 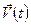в неограниченном объеме идеальной несжимаемой жидкости. Движение жидкости, вызванное движением сферы относительно этой системы отсчета, будем называть “абсолютным” движением.

Изучать “абсолютное” движение жидкости будем, пользуясь подвижной системой координат 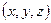, которая жестко скреплена со сферой и имеет начало в ее центре.

Возмущенное движение жидкости будет потенциальным, если оно непрерывно и возникло из состояния покоя. Потенциал 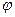в силу уравнения неразрывности для несжимаемой жидкости должен удовлетворять уравнению Лапласа всюду вне сферы,

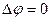(7.50)

со следующими добавочными условиями: в бесконечности жидкость покоится, и, следовательно,

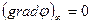, (7.51)

на поверхности сферы 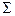должно выполняться условие непроницаемости и безотрывности течения жидкости (нормальная составляющая скорости 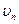жидкости должна равняться нормальной составляющей скорости точек поверхности сферы ).

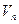Если сфера движется поступательно со скоростью 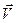вдоль оси 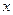, то условие обтекания (непроницаемости) запишется следующим образом:

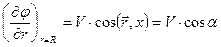, (7.52)

где 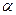– переменный угол между 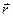и .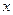

Решение поставленной задачи единственно и его легко получить на основе частных решений уравнения Лапласа.

Положим, что

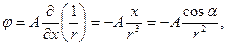(7.53)

где – некоторая постоянная. Так подобранная функция 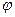удовлетворяет вне сферы уравнению Лапласа и в бесконечности стремится к нулю вместе со своими производными, т.е. удовлетворяет граничному условию в бесконечности.

Теперь необходимо так подобрать значение постоянной , чтобы удовлетворить и граничному условию непроницаемости (7.52). На поверхности сферы, очевидно,

Подставляя это значение в (7.52), получим

,

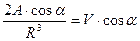т.е. условие (7.52) будет удовлетворено, если принять

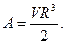
Таким образом, функция

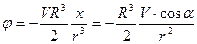(7.54)

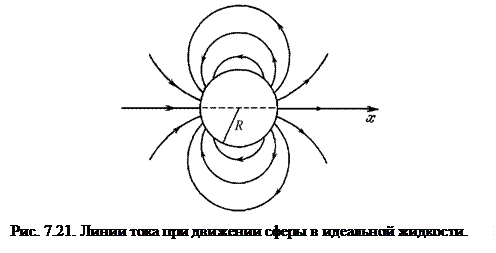
дает решение поставленной задачи о движении сферы в жидкости. На рис. 7.21 показаны линии тока построенного течения. Если сфера движется поступательно со скоростью, направленной произвольно относительно осей координат, то для потенциала скоростей возмущенного движения жидкости будет верна формула

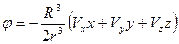. (7.55)

В общем случае при произвольных движениях сферы как твердого тела (поступательных и вращательных) потенциал скоростей представляется формулой (7.55), в которой 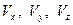являются компонентами скорости центра сферы в подвижных осях.

Для определения распределения давлений по поверхности сферы необходимо воспользоваться интегралом Коши – Лагранжа. При поступательном движении вдоль оси 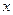, когда функция 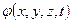определена в подвижной системе координат (см. (7.35’)), имеем

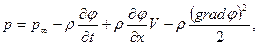(7.56)

где функция 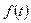уже определена на основании данных в бесконечно удаленной точке, в которой принято, что 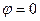, 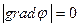и 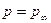. Зная распределение давления по поверхности 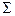, можно найти силу, действующую со стороны жидкости на сферу.

Рассмотрим задачу об обтекании неподвижной сферы потоком идеальной несжимаемой жидкости. Пусть скорость потока в бесконечности равна 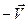и направлена параллельно оси 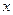. Движение жидкости в этом случае можно назвать “относительным”. Потенциал скоростей 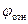должен всюду вне сферы удовлетворять уравнению Лапласа

и следующим граничным условиям: в бесконечности

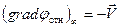
и на поверхности 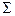сферы

.

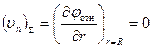Для получения решения этой задачи воспользуемся решением предыдущей задачи о движении сферы в неподвижной жидкости. Легко видеть, что решение задачи об обтекании сферы можно получить, если всей системе жидкость плюс сфера в предыдущей задаче сообщить скорость 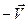, где 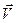– скорость движения сферы. Сфера при этом остановится, а на имевшееся ранее движение жидкости наложится поступательный поток, параллельный оси 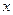, потенциал которого .

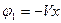Потенциал полученного таким образом течения

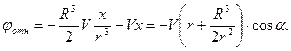(7.57)

будет гармонической функцией, удовлетворяющей как условию в бесконечности, так и условию на поверхности сферы.

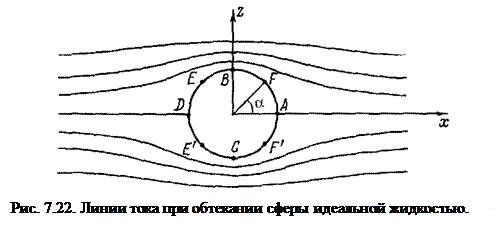
Таким образом, формула (7.57) дает решение поставленной задачи. Линии тока этого течения представлены на рис. 7.22. Поверхность сферы в этом случае является поверхностью тока.

Найдем распределение “относительных” скоростей по поверхности сферы

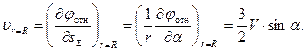(7.58)

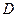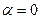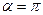Таким образом, в точках и (рис. 7.22), где и , скорость 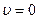, т.е. это – критические точки. Самая большая скорость достигается пр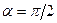и и 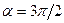(эта скорость равна 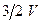, т.е. в полтора раза больше скорости набегающего потока).

Зная распределение скоростей по поверхности сферы, можно вычислить распределение давлений. Если скорость 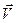не зависит от времени (движение установившееся), то можно воспользоваться интегралом Бернулли:

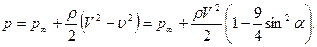(7.59)

Если скорость 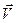постоянна, то распределение давлений на сфере одинаково в “абсолютном” и “относительном” движении (см. 7.56) и его можно вычислить по формуле (7.59). Из формулы (7.59) следует, что давления в симметричных точках одинаковы. Отсюда ясно, что суммарная сила, действующая со стороны жидкости на обтекаемую сферу, точно равна нулю. Сфера не испытывает сопротивления, подъемная сила также равна нулю.

Этот результат, известный под названием парадокса Даламбера, справедлив не только для сферы, но и для любого конечного тела произвольной формы, движущегося с постоянной скоростью в идеальной жидкости при отсутствии отрыва от поверхности тела и при условии, что скорость жидкости в бесконечности равна нулю. Парадокс устраняется тем, что в действительности безотрывное движение жидкости около сферы не осуществляется. С поверхности сферы сходят вихри, картина течения видоизменяется и нарушается симметрия в распределении давлений по передней и задней частям поверхности сферы.

Рассмотрим теперь случай, когда центр сферы движется в жидкости прямолинейно вдоль оси 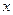с переменной скоростью. В этом случае движение жидкости неустановившееся, и для распределения давлений можно воспользоваться интегралом Коши – Лагранжа в форме (7.56), а для потенциала скоростей жидкости – формулой (7.54).

Видно, что при вычислении суммарной силы в формуле (7.56) необходимо использовать только член

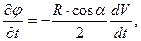
т.к. остальные члены дают части давления, одинаковые в симметричных точках сферы.

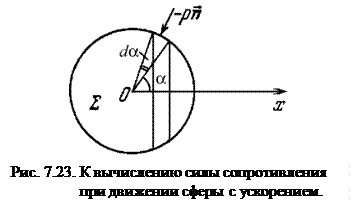Разбив поверхность сферы на элементарные полоски (рис. 7.23) с площадью 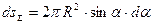и проводя интегрирование по всей поверхности сферы, для силы, действующей на сферу со стороны жидкости, получим следующее выражение:

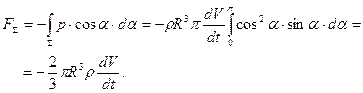(7.60)

Составим уравнение движения в проекции на ось 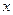для шара массы 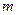, на который действует, кроме силы 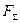со стороны жидкости, некоторая внешняя сила 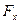. Будем иметь

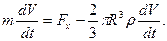
Обозначив 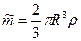, перепишем это уравнение в виде

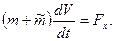
Отсюда следует, что сфера в жидкости будет двигаться под действием некоторых внешних сил 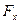так же, как она двигалась бы под действием этих сил в пустоте, если бы ее масса изменилась на 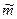. Величина 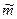называется присоединенной массой сферы. Она равна половине массы жидкости, вытесненной сферой. Присутствие внешней среды (в нашем случае – жидкости) сводится только к увеличению инерции шара.