Силы вязкого трения. Ламинарное и турбулентное
До сих пор в текущей главе мы рассматривали движение жидкостей и газов в пренебрежении силами вязкого трения. Между тем эти силы, действующие между частицами движущейся жидкости, могут кардинальным образом повлиять как на распределение скоростей в потоке жидкости, так и на обтекание жидкостью тел, помещенных в движущийся поток. Вблизи поверхности твердого тела возникает так называемый пограничный слой жидкости (см. § 13 текущей главы), в котором скорость нарастает от нуля до значения скорости в потоке. Влияние вязкости на движение остальной части жидкости мало. Но если, например, вязкая жидкость движется по достаточно узкой трубе, то пограничный слой может заполнить весь объем текущей жидкости и при изучении этого движения пренебрегать вязкостью нельзя. Такое течение имеет очень мало общего с движением идеальной жидкости.
При течении жидкости между ее отдельными слоями возникают тормозящие силы 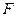 или касательные напряжения
или касательные напряжения 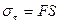 , где
, где 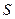 – площадь соприкосновения слоев. В результате взаимодействия слоев жидкости, их скорости
– площадь соприкосновения слоев. В результате взаимодействия слоев жидкости, их скорости 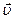 в направлении
в направлении 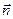 поперек потока изменяются от слоя к слою.
поперек потока изменяются от слоя к слою.
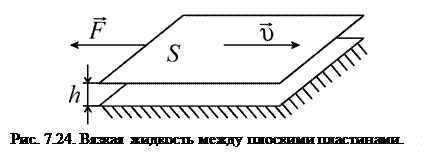
Еще Ньютон установил опытным путем, что при скольжении друг относительно друга двух параллельных плоскостей, пространство между которыми заполнено жидкостью, силы вязкого трения препятствуют этому скольжению (рис. 7.24). Так, при движении со скоростью 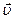 верхней плоскости относительно нижней возникает сила вязкого трения, направленная против движения и равная
верхней плоскости относительно нижней возникает сила вязкого трения, направленная против движения и равная
 .
.
Эта формула справедлива, если расстояние  между пластинами значительно меньше их линейных размеров
между пластинами значительно меньше их линейных размеров 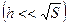 . Подчеркнем, что благодаря эффекту “прилипания” жидкости к поверхности пластины эта сила характеризует внутреннее трение, т.е. трение между проскальзывающими относительно друг друга слоями жидкости, а не между жидкостью и твердым телом.
. Подчеркнем, что благодаря эффекту “прилипания” жидкости к поверхности пластины эта сила характеризует внутреннее трение, т.е. трение между проскальзывающими относительно друг друга слоями жидкости, а не между жидкостью и твердым телом.
 |
Таким образом, сила трения между слоями текущей жидкости пропорциональна модулю градиента скорости по нормали 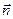 к площадке
к площадке 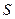 :
:
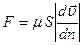 , (7.61)
, (7.61)
где 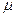 – коэффициент динамической вязкости.
– коэффициент динамической вязкости.
Внутреннее трение создается благодаря столкновениям молекул, которые приводят к замедлению или убыстрению движения среды. На основании кинетической теории газов, мера внутреннего сопротивления движению слоев жидкости, выраженная через коэффициент вязкости, определяется соотношением
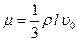 ,
,
где 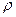 – плотность жидкости (газа),
– плотность жидкости (газа), 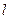 – средняя длина свободного пробега,
– средняя длина свободного пробега,  – средняя скорость теплового движения молекул. Размерность коэффициента динамической вязкости
– средняя скорость теплового движения молекул. Размерность коэффициента динамической вязкости 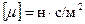 , единица измерения в СИ:
, единица измерения в СИ: 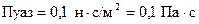 .
.
Вводится также кинематический коэффициент вязкости 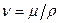 . Чтобы подчеркнуть молекулярную природу вязких сил, коэффициент кинематической вязкости нередко называют коэффициентом молекулярной вязкости. Размерность
. Чтобы подчеркнуть молекулярную природу вязких сил, коэффициент кинематической вязкости нередко называют коэффициентом молекулярной вязкости. Размерность 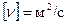 , единица измерения в СИ:
, единица измерения в СИ: 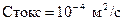 .
.
На основании опытов утверждается, что вязкость жидкости снижается с ростом температуры по логарифмическому закону:
 ,
,
где 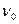 – коэффициент кинематической вязкости при
– коэффициент кинематической вязкости при 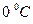 ,
, 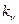 – множитель, характеризующий изменение кинематической вязкости в зависимости от температуры и рода жидкости. С повышением давления вязкость жидкости увеличивается, однако зависимость от давления сказывается только при больших перепадах давления – порядка десятков и сотен атмосфер. Необходимо заметить, что вязкость действует только при движении жидкости. При равновесии, т.е. для покоящихся жидкостей, влияние вязких сил не проявляется.
– множитель, характеризующий изменение кинематической вязкости в зависимости от температуры и рода жидкости. С повышением давления вязкость жидкости увеличивается, однако зависимость от давления сказывается только при больших перепадах давления – порядка десятков и сотен атмосфер. Необходимо заметить, что вязкость действует только при движении жидкости. При равновесии, т.е. для покоящихся жидкостей, влияние вязких сил не проявляется.
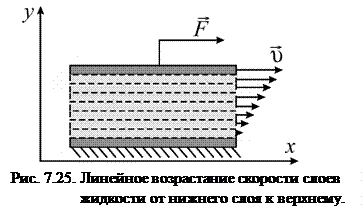 |
Представим, что жидкость между пластинами состоит из плоских параллельных слоев, движущихся равномерно (рис. 7.25). Каждый вышележащий слой увлекает за собой нижний соседний слой с силой  . В свою очередь, этот нижний слой тормозит движение верхнего слоя с той же по модулю силой. Таким образом, на каждый слой действуют сверху и снизу две равные, но противоположно направленные силы. Скорость слоев возрастает от нижнего слоя к верхнему линейно, а силы трения, действующие на каждый из слоев, одинаковы. Как результат, усилие, приложенное к верхней пластине, передается на нижнюю пластину.
. В свою очередь, этот нижний слой тормозит движение верхнего слоя с той же по модулю силой. Таким образом, на каждый слой действуют сверху и снизу две равные, но противоположно направленные силы. Скорость слоев возрастает от нижнего слоя к верхнему линейно, а силы трения, действующие на каждый из слоев, одинаковы. Как результат, усилие, приложенное к верхней пластине, передается на нижнюю пластину.
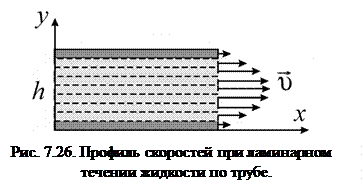
Рассмотрим течение вязкой жидкости между двумя неподвижными горизонтальными пластинами, расстояние между которыми равно  , под действием сил давления. Поскольку частицы жидкости “прилипают” к пластинам, то скорости слоев жидкости будут различными. Качественное распределение скоростей слоев изображено на рис. 7.26. Если известна характерная скорость течения (например, скорость
, под действием сил давления. Поскольку частицы жидкости “прилипают” к пластинам, то скорости слоев жидкости будут различными. Качественное распределение скоростей слоев изображено на рис. 7.26. Если известна характерная скорость течения (например, скорость 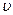 на оси потока), то легко оценить силы вязкого трения, приложенные к единичному объему (см. § 10 текущей главы):
на оси потока), то легко оценить силы вязкого трения, приложенные к единичному объему (см. § 10 текущей главы):
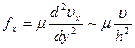 , (7.62)
, (7.62)
откуда следует, что силы вязкого трения убывают с увеличением расстояния между пластинами. В общем случае можно считать, что силы вязкости, возникающие в потоке, обратно пропорциональны квадрату характерного поперечного размера потока и пропорциональны скорости.
 |
С точки зрения динамики (см. уравнение Навье – Стокса для вязкой несжимаемой жидкости (4.49)), при отсутствии внешних сил  вязкостью можно пренебречь, если силы давления
вязкостью можно пренебречь, если силы давления 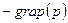 значительно превосходят силы вязкости
значительно превосходят силы вязкости 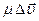 . Этот случай соответствует ускоренному движению жидкости, например, течению идеальной жидкости по горизонтальной трубе переменного сечения.
. Этот случай соответствует ускоренному движению жидкости, например, течению идеальной жидкости по горизонтальной трубе переменного сечения.
Следует, однако, подчеркнуть, что ламинарное течение жидкости, рассматриваемое в ряде случаев как идеальное, обязано наличию вязкости. В отсутствии вязкости течение жидкости будет неустойчивым. В самом деле, из-за флуктуаций скорости частиц линии тока стремятся искривиться, и частицы в них будут двигаться с ускорением. Давления 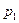 и
и 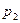 по разные стороны изогнутой трубки тока будут различными:
по разные стороны изогнутой трубки тока будут различными: 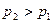 (рис. 7.27). Возникающий градиент давления связан с ускорением частиц жидкости уравнением
(рис. 7.27). Возникающий градиент давления связан с ускорением частиц жидкости уравнением
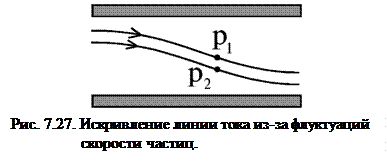
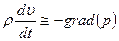 . (7.63)
. (7.63)
 |
Уравнение (7.63) является приближенным уравнением Навье – Стокса 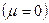 и записано в отсутствии внешних сил. В этом случае критерий малости сил вязкости сводится к неравенству
и записано в отсутствии внешних сил. В этом случае критерий малости сил вязкости сводится к неравенству
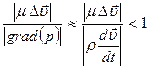 . (7.64)
. (7.64)
В гидродинамике очень часто используют понятие силы инерции 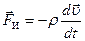 . С точки зрения наблюдателя, движущегося вместе с частицей жидкости, она находится в покое, потому что силы давления, вязкости и инерции уравновешивают друг друга (см. (4.49)):
. С точки зрения наблюдателя, движущегося вместе с частицей жидкости, она находится в покое, потому что силы давления, вязкости и инерции уравновешивают друг друга (см. (4.49)):
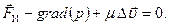
Неравенство (7.64) означает, что силы вязкости значительно меньше сил инерции. В случае течения жидкости между пластинами силы инерции при искривлении трубок тока жидкости
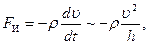 (7.65)
(7.65)
где 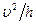 – характерное центростремительное ускорение. В общем случае силы инерции обратно пропорциональны поперечному размеру потока и пропорциональны квадрату скорости. С учетом оценок (7.62) и (7.65) условие (7.64) перепишется так:
– характерное центростремительное ускорение. В общем случае силы инерции обратно пропорциональны поперечному размеру потока и пропорциональны квадрату скорости. С учетом оценок (7.62) и (7.65) условие (7.64) перепишется так:
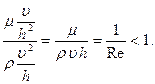 (7.66)
(7.66)
Здесь 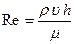 – число Рейнольдса, характеризующее отношение сил инерции и вязкости. Это число было открыто в 1883 г. О. Рейнольдсом и потому носит его имя. Оно характеризует переход от ламинарного течения к турбулентному в пограничном слое. Идеальной жидкости без трения соответствует число Рейнольдса, равное бесконечности
– число Рейнольдса, характеризующее отношение сил инерции и вязкости. Это число было открыто в 1883 г. О. Рейнольдсом и потому носит его имя. Оно характеризует переход от ламинарного течения к турбулентному в пограничном слое. Идеальной жидкости без трения соответствует число Рейнольдса, равное бесконечности 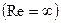 .
.
Таким образом, текущую жидкость можно рассматривать как невязкую, если число Рейнольдса для такого течения  . Однако и в этом случае вязкость играет вспомогательную роль. При не очень высоких скоростях течения силы вязкости “гасят” компоненты скорости жидкости, поперечные к потоку, препятствуя тем самым возникновению неустойчивого течения и обеспечивая ламинарность потока. Следовательно, сила инерции играет роль фактора, дестабилизирующего характер движения жидких частиц, а вязкость, наоборот, оказывает стабилизирующее влияние на поток.
. Однако и в этом случае вязкость играет вспомогательную роль. При не очень высоких скоростях течения силы вязкости “гасят” компоненты скорости жидкости, поперечные к потоку, препятствуя тем самым возникновению неустойчивого течения и обеспечивая ламинарность потока. Следовательно, сила инерции играет роль фактора, дестабилизирующего характер движения жидких частиц, а вязкость, наоборот, оказывает стабилизирующее влияние на поток.
Приведем некоторые оценки течения жидкости по круглой трубе радиуса 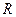 . Число Рейнольдса в этом случае
. Число Рейнольдса в этом случае 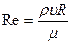 . Если принять радиус трубы
. Если принять радиус трубы 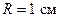 и скорость течения
и скорость течения  , то для воды (
, то для воды ( ,
, 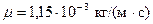 при
при 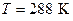 ) число
) число 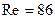 . Это означает, что силы вязкости не существенны, и воду можно рассматривать как невязкую жидкость. Однако это приближение становится несправедливым, если радиус трубки уменьшить на два порядка, и
. Это означает, что силы вязкости не существенны, и воду можно рассматривать как невязкую жидкость. Однако это приближение становится несправедливым, если радиус трубки уменьшить на два порядка, и 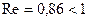 . При таком течении распределение давлений и скоростей в потоке уже не подчиняется уравнению Бернулли. При течении воздуха по трубе число Рейнольдса приблизительно на порядок меньше его значения для воды. Это указывает на то, что силы вязкости при течении воздуха и других газов оказывают более сильное влияние, чем при течении воды.
. При таком течении распределение давлений и скоростей в потоке уже не подчиняется уравнению Бернулли. При течении воздуха по трубе число Рейнольдса приблизительно на порядок меньше его значения для воды. Это указывает на то, что силы вязкости при течении воздуха и других газов оказывают более сильное влияние, чем при течении воды.
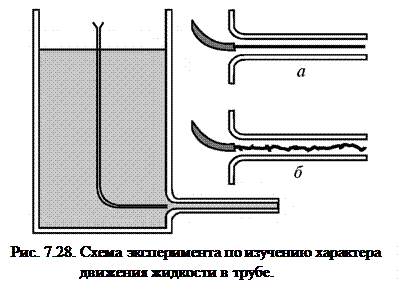
Стимулом к установлению двух режимов течения жидкостей послужила задача, в которой требовалось определить сопротивление потоку воды в круглой трубе. Английский инженер-физик О. Рейнольдс проводил опыты по определению сопротивления потоку жидкости, текущей в трубе. Из данных его эксперимента следовало, что при относительно высоких скоростях потока величина гидравлического сопротивления заметно расходилась с результатами расчетов, полученными для модели вязкой жидкости. Более того, характер движения жидкости при больших скоростях резко отличался оттого, что наблюдался в низкоскоростных потоках. Для детального изучения особенностей течения был поставлен следующий эксперимент (рис. 7.28).
Пусть жидкость вытекает из сосуда через горизонтальную стеклянную трубку. Для контроля над характером течения при помощи капилляра впускают ту же, но окрашенную жидкость во входное отверстие трубки.
В случае малого поперечного сечения трубки и не очень большой скорости течения окрашенная струйка движется прямолинейно строго вдоль оси трубки (рис. 7.28 а). При большем сечении или при увеличении скорости наблюдается нерегулярное движение, когда струйка разбивается на множество извилистых струек (рис. 7.28 б). В первом случае движение называется слоистым (ламинарным), а во втором – турбулентным. При ламинарном течении силы вязкости сглаживают боковые движения жидкости, возникающие вследствие флуктуаций и различных неровностей стенок трубы. При недостаточной вязкости случайные боковые движения жидкости усиливаются, способствуя тем самым возникновению турбулентности.
Переход от ламинарного течения к турбулентному происходит при некотором числе Рейнольдса, получившем название критического:
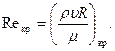 (7.67)
(7.67)
Значение этого критического числа сильно зависит от формы входной части трубы. В случае закругленного конца, как показано на рис. 7.28, течение остается ламинарным вплоть до больших чисел Рейнольдса. Область критических чисел 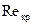 лежит между значениями 1200 (незакругленный вход) и 20000 (закругленный вход).
лежит между значениями 1200 (незакругленный вход) и 20000 (закругленный вход).
 |
Для круглой трубы критическое число Рейнольдса, определяющее переход от ламинарного к турбулентному режиму течения, как показали эксперименты, равно 2300. Когда параметры течения были таковы, что число Рейнольдса достигало значений, превышающих эту величину, поток в трубе становился турбулентным. При числах Рейнольдса, меньших этой величины, движение частиц оставалось ламинарным. В более детальных экспериментах было установлено, что граница смены режима зависит от того, с какой стороны осуществляется развитие потока – от турбулентного или ламинарного.
Оказалось, что переход к турбулентному течению от ламинарного может быть затянут до чисел Рейнольдса порядка 50000. Но со стороны турбулентного движения переход к ламинарному течению наступал всегда при числах Рейнольдса, равных 2300. В различных типах течения ламинарное движение переходит в турбулентное при разных значениях чисел Рейнольдса. В частности, в реках турбулентный режим движения воды наступает при числах Рейнольдса, подсчитываемых по поперечному сечению русла, равных 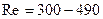 .
.
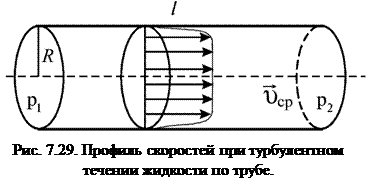
При стационарном (установившемся) турбулентном движении скорость жидкости в данном месте не остается постоянной, а совершает хаотические колебания и по модулю, и по направлению. Но средняя скорость  в данном месте трубы будет постоянна и направлена вдоль оси трубы. В турбулентном потоке (рис. 7.29) можно четко выделить пограничный слой жидкости вблизи стенок трубы, где средняя скорость быстро спадает до нуля, в то время как при ламинарном течении такого четкого пограничного слоя нет, т.к. скорость изменяется за счет вязкости по всему сечению трубы. На практике для расчета турбулентного течения жидкости по трубе используется формула
в данном месте трубы будет постоянна и направлена вдоль оси трубы. В турбулентном потоке (рис. 7.29) можно четко выделить пограничный слой жидкости вблизи стенок трубы, где средняя скорость быстро спадает до нуля, в то время как при ламинарном течении такого четкого пограничного слоя нет, т.к. скорость изменяется за счет вязкости по всему сечению трубы. На практике для расчета турбулентного течения жидкости по трубе используется формула
 , (7.68)
, (7.68)
где 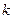 – безразмерный гидравлический коэффициент.
– безразмерный гидравлический коэффициент.
Средняя же по сечению скорость ламинарного течения получается равной (см. формулу Пуазейля, § 10)
 ,
,
откуда разность давлений как функция скорости определяется формулой
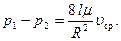 (7.69)
(7.69)
Сравнивая перепады давлений для турбулентного (7.68) и ламинарного (7.69) течений, можно заключить, что повышение скорости прокачки жидкости по трубам при турбулентном течении потребует значительно большего увеличения перепада давлений, чем при ламинарном.
 |
При свободном ламинарном течении жидкости (в отсутствии направляющих поверхностей) развиваются неустойчивости, и ламинарное течение переходит в турбулентное. На рис. 7.30 представлено изображение струи жидкости 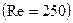 . Хорошо видно, что течение от ламинарного режима через переходный трансформируется в турбулентный. До настоящего времени нет ясного понимания всех стадий развития турбулентности. Классическая линейная теория устойчивости дает качественно верное описание начальной стадии разрушения ламинарности. Ясно, что переход к турбулентному течению является существенно нелинейным процессом, и теория устойчивости должна базироваться на анализе нелинейных уравнений гидродинамики.
. Хорошо видно, что течение от ламинарного режима через переходный трансформируется в турбулентный. До настоящего времени нет ясного понимания всех стадий развития турбулентности. Классическая линейная теория устойчивости дает качественно верное описание начальной стадии разрушения ламинарности. Ясно, что переход к турбулентному течению является существенно нелинейным процессом, и теория устойчивости должна базироваться на анализе нелинейных уравнений гидродинамики.
 |
Известно, что поток реальной жидкости или газа действует с некоторой силой на тело, помещенное в этот поток. Для осесимметричного тела с осью симметрии, направленной вдоль потока, эта сила также будет направлена вдоль потока. Она получила название силы лобового сопротивления,  .
.
Эта сила возрастает с увеличением скорости потока аналогично росту перепада давлений при увеличении скорости течения жидкости по трубе. Основные физические причины возникновения лобового сопротивления можно установить, если рассмотреть обтекание потоком шара радиуса 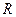 . На рис. 7.31 изображена зависимость силы лобового сопротивления от числа Рейнольдса
. На рис. 7.31 изображена зависимость силы лобового сопротивления от числа Рейнольдса 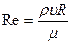 .
.
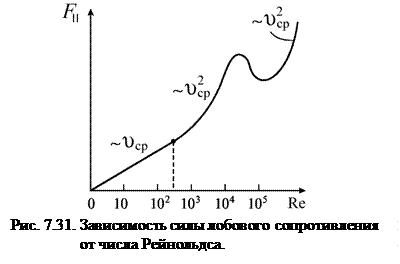
При малых скоростях течения, когда 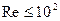 ,
, 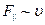 . Это происходит потому, что на шар действуют силы вязкости, возникающие вследствие существования тонкого пограничного слоя вблизи поверхности шара. При таких скоростях происходит ламинарное течение жидкости. В настоящее время хорошо развита теория пограничного слоя, которая, в частности, позволяет оценить его толщину по формуле
. Это происходит потому, что на шар действуют силы вязкости, возникающие вследствие существования тонкого пограничного слоя вблизи поверхности шара. При таких скоростях происходит ламинарное течение жидкости. В настоящее время хорошо развита теория пограничного слоя, которая, в частности, позволяет оценить его толщину по формуле
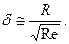 (7.70)
(7.70)
Линейный участок кривой, изображенной на рис. 7.31, оканчивается при числах Рейнольдса 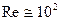 . Для таких чисел Рейнольдса толщина пограничного слоя на порядок меньше радиуса шара. Вне этого слоя реальная жидкость течет так же, как и идеальная, обтекая шар симметрично. Наоборот, при числах
. Для таких чисел Рейнольдса толщина пограничного слоя на порядок меньше радиуса шара. Вне этого слоя реальная жидкость течет так же, как и идеальная, обтекая шар симметрично. Наоборот, при числах 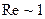 говорить о пограничном слое некорректно, т.к. градиенты скорости существенны в области, размеры которой значительно больше радиуса шара.
говорить о пограничном слое некорректно, т.к. градиенты скорости существенны в области, размеры которой значительно больше радиуса шара.
 |
При малых числах Рейнольдса сила лобового сопротивления для шара подчиняется закону Стокса:
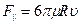 . (7.71)
. (7.71)
Используя (7.71), можно измерить вязкость жидкости, наблюдая за движением тел в этой жидкости. Так, при падении шарика в жидкости его скорость изменяется в соответствии с уравнением
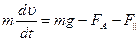 , (7.72)
, (7.72)
где 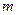 – масса шарика,
– масса шарика, 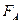 – выталкивающая сила (сила Архимеда),
– выталкивающая сила (сила Архимеда),  – сила вязкого трения, определяемая формулой (7.71).
– сила вязкого трения, определяемая формулой (7.71).
По истечении некоторого промежутка времени шарик приобретет максимальную скорость, с которой он практически равномерно будет падать вниз. Измерив в эксперименте скорость падающего шарика, из (7.72) с учетом того, что при установившемся движении шарика 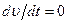 , выражают вязкость жидкости
, выражают вязкость жидкости 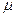 :
:
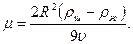 (7.73)
(7.73)
Так, например, скорость падения стального шарика радиусом 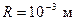 в глицерине при
в глицерине при 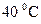 равна
равна 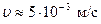 , и вязкость
, и вязкость 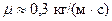 . Указанной скорости соответствует число Рейнольдса
. Указанной скорости соответствует число Рейнольдса  , поэтому здесь отсутствует пограничный слой.
, поэтому здесь отсутствует пограничный слой.
При скоростях потока, когда 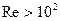 , симметрия обтекания нарушается – позади шара происходит отрыв линий тока (рис. 7.32). При таких скоростях пограничный слой становится очень тонким, а поперечные градиенты скорости в нем – большими. Силы вязкости, которые при этом возрастают, тормозят движение частиц среды, движущихся вдоль поверхности шара настолько, что они не в состоянии полностью обогнуть шар. Хотя течение в тонком пограничном слое остается ламинарным, позади шара образуются вихри. Симметрия давлений в точках
, симметрия обтекания нарушается – позади шара происходит отрыв линий тока (рис. 7.32). При таких скоростях пограничный слой становится очень тонким, а поперечные градиенты скорости в нем – большими. Силы вязкости, которые при этом возрастают, тормозят движение частиц среды, движущихся вдоль поверхности шара настолько, что они не в состоянии полностью обогнуть шар. Хотя течение в тонком пограничном слое остается ламинарным, позади шара образуются вихри. Симметрия давлений в точках  и
и 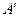 нарушается. Спереди шара течение такое же, как и в отсутствии трения, поэтому давление в точке
нарушается. Спереди шара течение такое же, как и в отсутствии трения, поэтому давление в точке 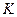
 .
.
Однако в точке 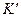 давление
давление 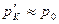 . Поэтому результирующая сила давления, действующая на шар в направлении потока, будет пропорциональна гидродинамическому напору
. Поэтому результирующая сила давления, действующая на шар в направлении потока, будет пропорциональна гидродинамическому напору 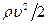 и площади поперечного сечения шара
и площади поперечного сечения шара 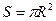 . На практике силу лобового сопротивления вычисляют по формуле
. На практике силу лобового сопротивления вычисляют по формуле
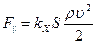 , (7.74)
, (7.74)
где 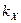 – коэффициент лобового сопротивления для тела данной формы. Область квадратичной зависимости силы
– коэффициент лобового сопротивления для тела данной формы. Область квадратичной зависимости силы  от скорости
от скорости 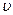 простирается вплоть до чисел Рейнольдса
простирается вплоть до чисел Рейнольдса 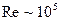 . При больших скоростях пограничный слой постепенно турбулизуется, и при
. При больших скоростях пограничный слой постепенно турбулизуется, и при 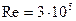 он полностью турбулентен. В области постепенной турбулизации пограничного слоя сила сопротивления с ростом скорости даже несколько уменьшается, поскольку сокращается область срыва потока. Однако затем квадратичная зависимость (7.74) опять восстанавливается, с несколько меньшим коэффициентом
он полностью турбулентен. В области постепенной турбулизации пограничного слоя сила сопротивления с ростом скорости даже несколько уменьшается, поскольку сокращается область срыва потока. Однако затем квадратичная зависимость (7.74) опять восстанавливается, с несколько меньшим коэффициентом 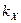 .
.
 |
Для ламинарного и турбулентного обтекания тел можно использовать единую формулу для расчета силы лобового сопротивления
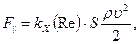 (7.75)
(7.75)
в которой коэффициент лобового сопротивления должен зависеть от скорости так, как это изображено на рис. 7.33.
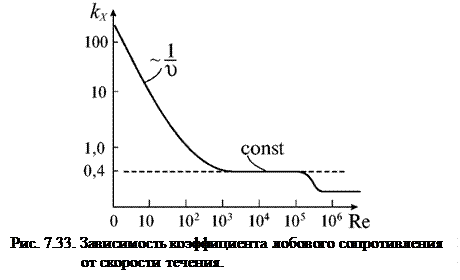 |
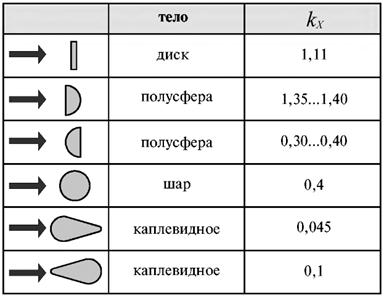
Ниже в таблице 7.1 представлены величины коэффициентов лобового сопротивления для тел различной формы. Видно, что наименьшим коэффициентом лобового сопротивления обладает осесимметричное каплевидное тело, у которого тупой нос и заостренная задняя часть. При обтекании этого тела поток хорошо смыкается позади него, препятствуя тем самым падению давления за телом.
Таблица 7.1. Коэффициенты лобового сопротивления.
 |

Если расположить цилиндр поперек потока, то на него будет действовать сила лобового сопротивления. Однако если цилиндр привести во вращение вокруг своей оси, то появится также и подъемная сила. Эта сила появляется вследствие вращения цилиндра в вязком воздухе. Само явление получило название эффекта Магнуса.
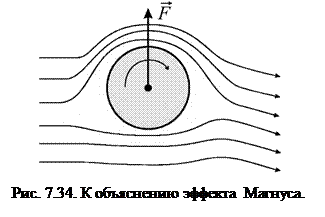
При вращении цилиндра воздух в пограничном слое увлекается поверхностью цилиндра. Обтекание вращающегося цилиндра будет выглядеть так, как показано на рис. 7.34. Скорость воздушного потока над цилиндром будет больше, чем под ним. Величина силы  , как показывает расчет, возрастает с увеличением как скорости потока, так и угловой скорости вращения цилиндра.
, как показывает расчет, возрастает с увеличением как скорости потока, так и угловой скорости вращения цилиндра.
 |
Эффект Магнуса не получил широкого технического применения. Однако в спортивных играх с мячом последний часто подкручивают, чтобы задать полету мяча нужную траекторию.
 2014-02-02
2014-02-02 14290
14290








