Очевидно, что разные МТ могут совершать разное перемещение D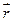 за одинаковое время Dt.
за одинаковое время Dt.
▼ Пусть МТ за время Dt совершило перемещение D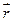 .
.  ср=D
ср=D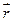 /Dt (1) назовем средней скоростью движения МТ за время Dt. Будем уменьшать Dt.
/Dt (1) назовем средней скоростью движения МТ за время Dt. Будем уменьшать Dt.
▼ По определению предел  =
=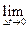
 ср=D
ср=D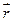 /Dt (2)(если он существует), называется мгновенной скоростью движения МТ в момент времени t, это вектор. Используя математическое определение производной, вторую часть формулы можно записать в следующем виде
/Dt (2)(если он существует), называется мгновенной скоростью движения МТ в момент времени t, это вектор. Используя математическое определение производной, вторую часть формулы можно записать в следующем виде  =
=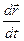 (3), т.е. ▼ мгновенная скорость есть первая производная
(3), т.е. ▼ мгновенная скорость есть первая производная 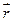 МТ от времени. Разложим (3) по формуле
МТ от времени. Разложим (3) по формуле 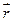 =x(t)
=x(t) x+y(t)
x+y(t) y+z(t)
y+z(t) z. (4) по правилам дифференцирования.
z. (4) по правилам дифференцирования.  x,
x,  y и
y и  z фиксированные в пространстве и поэтому они постоянны во времени.
z фиксированные в пространстве и поэтому они постоянны во времени.  =
=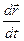 =
=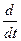 (x
(x x+ y
x+ y y+ z
y+ z z)=
z)=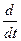 (x
(x x)+
x)+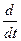 (y
(y y)+
y)+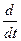 (z
(z z)=
z)= x
x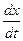 +
+ y
y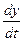 +
+ z
z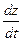 (5). С другой стороны
(5). С другой стороны  так же может быть разложен по формуле (4) в базисе
так же может быть разложен по формуле (4) в базисе  x,
x,  y и
y и  z:
z:  =
=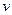 x
x x+
x+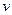 y
y y+
y+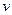 z
z z (6). Сравнивая (5) и (6) единством разложения вектора по базису получаем
z (6). Сравнивая (5) и (6) единством разложения вектора по базису получаем 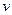 x=
x=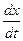 ,
, 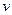 y=
y=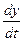 ,
, 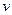 z=
z=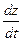 (7).
(7).
6.Ускорение МТ.
Понятно, что скорость также меняется во времени. Пример-разгон авто. Введем характеристику, описывающую скорость изменения скорости (временное изменение). Для этого рассмотрим отрезок траектории между двумя соседними точками М1 и М2, которые занимала МТ. В каждой точке  направлен по касательной к этой траектории. Введем разные векторы
направлен по касательной к этой траектории. Введем разные векторы  1 и
1 и  2 по формуле D
2 по формуле D =
= 2-
2- 1 (1).
1 (1).
▼ По определению вектор равный W=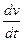 (2) (W=vj) называется вектором среднего ускорения за время Dt. Далее поступаем также как и с определением мгновенной скорости. Мгновенное ускорение МТ определяется как предел среднего ускорения (2)
(2) (W=vj) называется вектором среднего ускорения за время Dt. Далее поступаем также как и с определением мгновенной скорости. Мгновенное ускорение МТ определяется как предел среднего ускорения (2) 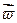 =
=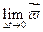 ср=
ср=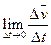 (3) если этот предел существует.
(3) если этот предел существует.
▼ Мгновенное ускорение определяется 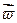 =
=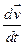 (4).
(4).  =
=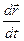 ,
, 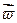 =
=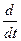 (
(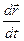 ) (5).
) (5).
▼ Выражение (5) обозначает вторую производную по времени от 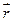 (производная от первой производной).
(производная от первой производной). 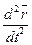 =
=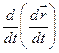 (6). Разобьем D
(6). Разобьем D =D
=D n+D
n+D τ (8) по построению (М1В=
τ (8) по построению (М1В=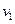 ), отвечает за удлинение вектора скорости МТ в процессе ее движения, а D
), отвечает за удлинение вектора скорости МТ в процессе ее движения, а D n отвечает за поворот D
n отвечает за поворот D в процессе движения МТ. Представим (8) в виде (3):
в процессе движения МТ. Представим (8) в виде (3): 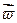 =
=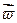 n+
n+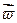 τ (9),
τ (9), 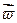 n=
n=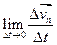 (10),
(10), 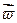 τ=
τ=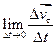 (11),
(11), 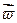 τ=
τ=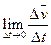 =
=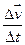 (12)
(12)
▼ 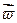 τ по величине хар-ет быстроту изменения величины скорости и очевидно, при Dt→0 сам
τ по величине хар-ет быстроту изменения величины скорости и очевидно, при Dt→0 сам 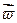 τ будет направлен по направлению скорости в этой точке, т.е. по касательной, по этой причине
τ будет направлен по направлению скорости в этой точке, т.е. по касательной, по этой причине 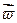 τ дназывается касательным или тангенсальным ускорением МТ. Рассмотрим И2, рассмотрим равнобедренный треугольник МАВ, Dα+2β=
τ дназывается касательным или тангенсальным ускорением МТ. Рассмотрим И2, рассмотрим равнобедренный треугольник МАВ, Dα+2β=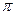 (13).
(13).
▼ 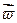 n – направленно
n – направленно 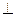 -но к вектору
-но к вектору  .(
.(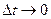 ,
,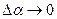 ,
,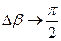 ) (14). Проведем в М1 и М2
) (14). Проведем в М1 и М2 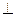 -ры к касательным. Они пересекаются в точке О. Для малых Dt, М1О
-ры к касательным. Они пересекаются в точке О. Для малых Dt, М1О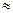 М2О=R (15).Рассмотрим DМ1М2О. R
М2О=R (15).Рассмотрим DМ1М2О. R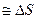 /
/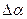 (17), R=
(17), R=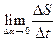 (18).
(18).
▼ Величина определяемая по формуле (18) называется радиусом кривизны траектории. Рассмотрим DМ1М2О DМ1АВ (они подобны). 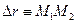 -величина перемещения (19).
-величина перемещения (19). 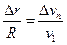 =>
=>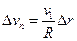 . (20).
. (20). 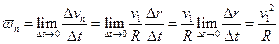 . Мы доказали
. Мы доказали 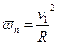
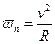 (21).
(21).
▼ 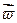 n –величина которая определяется формулой (21) и которая направлена перпендикулярно к касательной к траектории называется нормальным вектором ускорения.
n –величина которая определяется формулой (21) и которая направлена перпендикулярно к касательной к траектории называется нормальным вектором ускорения.
 2014-02-02
2014-02-02 1055
1055
