2014-02-02
1138
Рис. 4.54.
Рис. 4.53.
Рис. 4.52.
Рис. 4.51.
Рис. 4.50.
Рис. 4.49.
На рисунке точка М1 соответствуют режиму автоколебаний, а М2 – неустойчивым колебаниям.
ПРИМЕР
Пусть дана нелинейная система:
Параметры системы:
Линейная часть представлена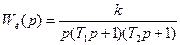 
, где k=0.4; T1=1 c; T2=5 c.
Нелинейный элемент имеет характеристику
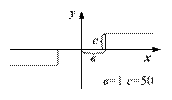
Определить есть ли в данной системе автоколебания. Если есть, то найти параметры входного воздействия, при котором в системе наблюдаются автоколебания.
Применим метод гармонической линеаризации:
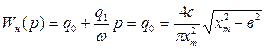
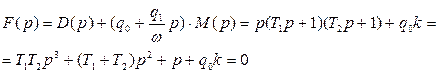
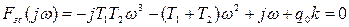
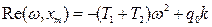
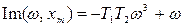
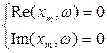
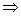
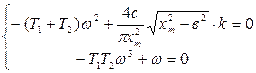
Найдем значение xm, ω.:
Из второго уравнения системы имеем:
=> 
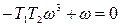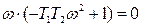
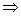
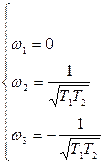
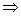
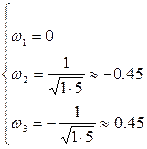
В системе возможны автоколебания при ω> 0, значит, они возможны только при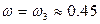 
Из первого уравнения системы найдем xm,соответствующие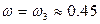
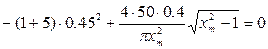
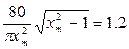
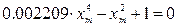
Разрешив биквадратное уравнение через замену переменной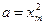 
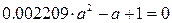
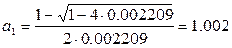
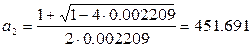
Получаем четыре корня:
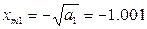
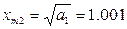
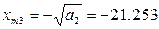
Очевидно, что при всех x m ограничения (1), (2) выполняются, при x m ≤0 в системе автоколебаний быть не может. Получилось 2 решения системы: (0.45;1.001) и (0.45;21.253). Для дополнительных исследований используем критерий Михайлова:
|
|
|
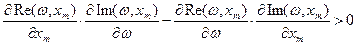
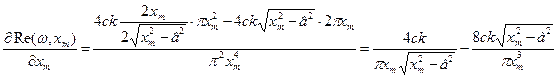
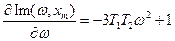
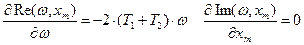
Проверим, выполняется ли неравенство (*) для полученных решений:
а). При ω =0.45 x m=1.001
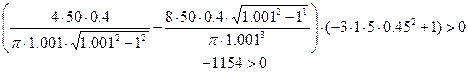
Как видно неравенство не выполняется, значит, при данных значениях в системе автоколебаний не будет.
б). При ω =0.45 x m=21.253
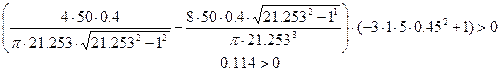
Неравенство выполняется, значит, при данных значениях входного сигнала в системе будут наблюдаться автоколебания. Промоделируем эту схему в MATLAB 5.1.
Полученная схема:
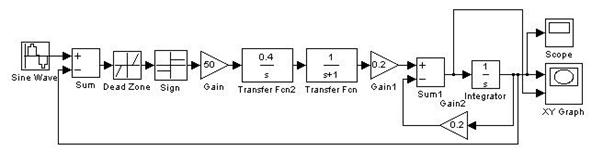
Выходной сигнал системы при значениях входного сигнала ω =0.45 x m=21.253:
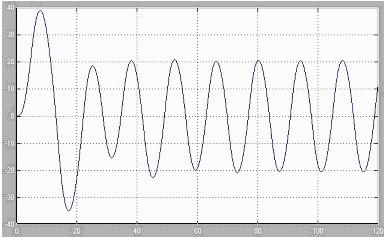
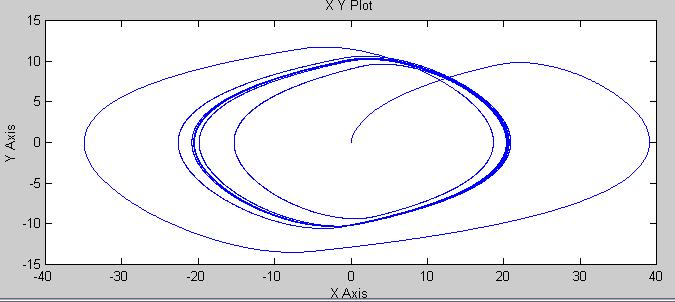
Фазовая траектория:
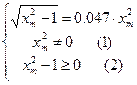
Критерий абсолютной устойчивости Попова дает достаточное условие абсолютной устойчивости нелинейной системы с одной однозначной нелинейностью.
Критерий Попова основан, как и критерий Найквиста, на использовании амплитудно-фазовой характеристики и имеет простую геометрическую интерпретацию.
Пусть в контуре нелинейной системы содержится нелинейный элемент с характеристикой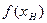 
, имеющей любую конфигурацию, но не выходящей за пределы определенного сектора [0, kH]
