Функциональные модели радиосистем

Функциональные модели занимают промежуточное положение между системотехническими и схемотехническими моделями. Им присуща большая конкретность в представлении процесса функционирования радиосистемы по сравнению с системотехническими моделями, что позволяет с их помощью уточнять требования к отдельным радиоустройствам, в то же время в них отсутствует излишняя детализация, свойственная схемотехническим моделям, что позволяет реализовать такие модели даже на персональных ЭВМ.

Функциональные модели отражают процесс функционирования реальной радиосистемы, представлением ее в виде набора функциональных блоков, каждый из которых выполняет заданную функцию по формированию или преобразованию радиосигналов или информационных процессов. Для математического моделирования на функциональном уровне радиосистему следует декомпозировать на ограниченное число таких функциональных блоков. При этом физические устройства могут и не совпадать с функциональными, на которые декомпозируется система. К функциональным блокам, например, можно отнести совокупность радиоустройств, осуществляющих генерирование информационных процессов и радиосигналов; устройств, осуществляющих прием и демодуляцию радиосигналов, и т.п. Располагая набором различных функциональных блоков, из них можно составлять функциональные модели широкого класса радиосистем. Очевидно, что декомпозиция реальной системы и составление функциональной модели требуют более детальных знаний о системе, чем при системотехническом подходе к моделированию. Для радиосистем определенного класса обычно реализуют адаптивное автоматизированное разбиение ее модели на функциональные блоки.

Алгоритмически функциональная модель радиосистемы представляет совокупность библиотеки функциональных блоков, подпрограммы-интерпретатора связей между ними, управляющей программы моделирования, осуществляющей продвижение имитационного времени и передачу управления на подпрограммы, имитирующие функционирование блоков, а также набора стандартных подпрограмм для организации вычислительного эксперимента, представления результатов моделирования и т.п.

Воздействия на входах и выходах функциональных блоков будут представлять собой фазовые переменные модели. Способ описания фазовых переменных существенно влияет на состав модели и макромодели функциональных блоков. Из используемых в настоящее время методов описания входных воздействий и фазовых переменных необходимо отметить следующие:

- метод несущей, когда используются мгновенные значения фазовых переменных, входных сигналов и их смеси с помехами ;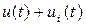

- метод комплексной огибающей, когда фазовые переменные и входные сигналы описываются с точностью до их комплексных огибающих ;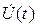

- метод статистических эквивалентов, когда реальные случайные процессы в радиосистеме представляются своими статистическими характеристиками, например математическим ожиданием, дисперсией и т.д., либо когда реальные процессы заменяются другими, но статистически адекватными им в рамках выбранного критерия, например по совпадению определенного числа моментов;

- метод информационного параметра, когда вместо исследования прохождения реального сигнала в модели системы изучается прохождение через модель информационного параметра, для приема и обработки которого эта система предназначена.

Независимо от способа описания фазовых переменных иразбиения модели системы на функциональные блоки макромодели отдельных функциональных блоков обычно представляют в виде динамических звеньев, чтобы проследить функционирование системы во времени. В самом общем случае в динамическом звене входные и выходные переменные связаны системой дифференциальных уравнений. В простейшем случае функционального блока с одним входом — выходом (рис. 9.7, а) при использовании метода несущей эта связь может быть записана в виде

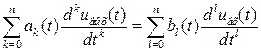. (9-10)

Уравнение (9.10) описывает линейное нестационарное звено с сосредоточенными постоянными. В случае стационарных звеньев 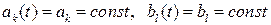и можно использовать не эту запись, а более простую запись связи входных и выходных переменных через обобщенные характеристики звена: импульсную 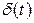, переходную 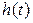, передаточную 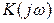и т.д., что позволяет при моделировании избежать интегрирования системы дифференциальных уравнений. Если звено, моделирующее функциональный блок, является стационарным и безынерционным, то (9.10) превращается в нелинейное уравнение:

Рис. 9.7. Модели функциональных блоков радиосистем

Если функциональный блок моделируется нелинейным динамическим звеном, то связь входных и выходных переменных может быть записана в виде системы нелинейных дифференциальных уравнений соответствующего порядка. Одномерные безынерционные нелинейные звенья (рис. 9.7, б) описываются нелинейной зависимостью 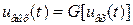, где функцию G стремятся аппроксимировать удобными для вычислений математическими формулами. Инерционное нелинейное звено обычно представляют в виде каскадного включения нелинейного безынерционного звена и линейного инерционного (рис. 9.7, в) для упрощения моделирования системы.

Для нахождения отклика системы на сложное входное воздействие в методе несущей при линейных моделях функциональных блоков обычно используется интеграл свертки. Если модели функциональных блоков нелинейны, то для определения отклика системы приходится решать систему нелинейных дифференциальных уравнений.

Дискреты продвижения имитационного времени при моделировании по методу несущей выбираются более жесткими, чем требует теорема Котельникова, так как для точного представления непрерывного процесса рядом его дискретных значений необходима специальная обработка дискретных выборок с помощью оптимальных фильтров. Такая обработка в ЭВМ не предусмотрена, и интервал дискретизации фазовых переменных выбирается из условия

,

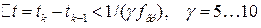где 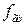— верхняя граничная частота спектра сигнала. При моделировании по методу несущей 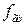определяется радиочастотами, на которых работает радиосистема, и поэтому значение 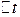оказывается малым, что затрудняет использование этого метода для моделирования больших систем.

Для примера рассмотрим функциональную модель оптической системы связи рис. 9.2, построенную по методу несущей. В качестве фазовых переменных, зависящих от времени, в модели системы рационально выбрать: 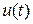- подлежащий передаче информационный случайный двоичный сигнал, 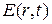- напряженность электрического поля световой волны в раскрыве передающей линзы, 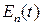- шумы открытого оптического канала связи, 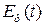- напряженность электрического ноля в раскрыве приемной линзы, 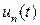- собственные шумы приемного устройства, 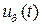- выходной сигнал фотоприемного устройства.

В качестве функциональных блоков выберем: передающее устройство вместе с оптикой, математическое описание функционирования моделирующего его звена на основании (9.3) имеет вид 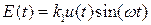( 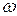- частота световой несущей); оптический канал, для моделирующего звена которого из (9.2) получим 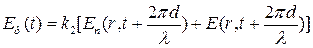; фотоприемное устройство, работа которого характеризуется следующим математическим выражением: 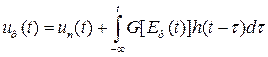, где 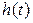— переходная характеристика выходного фильтра детектора, G — нелинейная функция детектора светового излучения, k ₁, k ₂— коэффициенты пропорциональности. Результирующая схема модели оптической системы связи, состоящая из набора перечисленных функциональных блоков, показана на рис. 9.8.

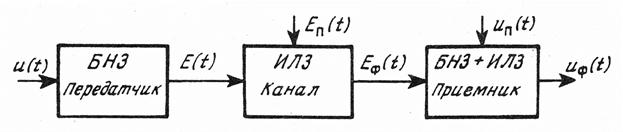
Рис. 9.8. Функциональная модель системы связи по методу несущей

При имитации управляющая программа моделирования для каждого момента имитационного времени t_i,связанного с тактами посылок двоичного сигнала, будет генерировать по заданным законам значения шумовых составляющих 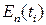, 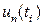и затем поочередно передавать управление подпрограммам, имитирующим работу звеньев, моделирующих функциональные блоки в соответствии с вышеприведенными выражениями по результатам моделирования можно будет оценить эффективность оптической системы связи и требуемые характеристики ее отдельных блоков.

При моделировании радиосистем по методу комплексной огибающей фазовые переменные представляются в виде их комплексных огибающих 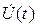, а модели функциональных блоков представляются эквивалентными низкочастотными и не всегда физически реализуемыми звеньями, выполняющими над огибающей радиосигнала ту же функцию, что и исходное звено над полным радиосигналом. Для моделирования методом комплексной огибающей разработан ряд методов описания функциональных блоков и фазовых переменных, Применительно к задачам радиотехники наиболее рационален метод, разработанный Евтяновым на основе метода медленно меняющихся амплитуд Ван-дер-Поля. При использовании этого метода любое динамическое звено может быть описано дифференциальным уравнением относительно комплексных медленно изменяющихся вместе с информационным процессом амплитуд 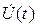. В случае линейного звена, как и в методе несущей, возможно использование переходных, импульсных или передаточных характеристик, записанных для комплексных огибающих. Связь между, например, переходными характеристиками функциональных блоков по методу несущей 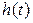и по методу комплексной огибающей 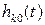определяется соотношением

,

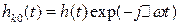где 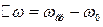, 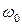— частота несущей, 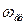- верхняя граничная частота спектра радиосигнала.

При моделировании по методу комплексной огибающей широко используются спектральные методы. В соответствии с теоремой смещения преобразования Фурье, если для переходной характеристики по методу несущей 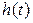передаточная функция звена равна 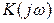(они, как известно, связаны преобразованием Фурье), для переходной характеристики по методу комплексной огибающей 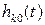передаточная функция будет равна

.

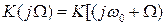Два последних выражения свидетельствуют, что уравнению, характеризующему функциональный блок по методу несущей в виде стационарного линейного радиозвена рис. 9.7, а, всегда соответствует уравнение модели эквивалентного блока для комплексной огибающей и нахождение его не составляет трудностей. Большую сложность вызывает отыскание уравнений для нелинейных звеньев, но и здесь разработаны эффективные методы для их определения [25].

При моделировании радиосистем по методу комплексной огибающей дискреты продвижения имитационного времени ограничиваются шириной спектра информационного сигнала, а так как информационные процессы протекают во много раз медленнее несущей, то этот метод допускает существенно большую скорость имитации, чем предыдущий, хотя и не столь универсален. Примеры математических моделей функциональных блоков радиосистем по методам несущей и комплексной огибающей приведены в [1, 17, 25].

При моделировании по методу статистических эквивалентов реальные случайные процессы на входах—выходах функциональных блоков заменяются другими процессами, имеющими такие же статистические характеристики. Таким образом, статистический эквивалент функционального блока обеспечивает лишь в статистическом смысле с точностью до выбранных статистических характеристик адекватность выходного сигнала реальному процессу.

В настоящее время известно много методов получения статистических эквивалентов моделей функциональных блоков радиосистем: статистической линеаризации, генерации, фильтрации информационного параметра и др., но наибольшее распространение получили различные варианты метода статистической линеаризации.

При использовании этого метода нелинейные динамические звенья, моделирующие функциональные блоки радиосистем, заменяются линейными, безынерционными, обеспечивающими совпадение заданных статистических характеристик входной и выходной фазовых переменных. Например, можно потребовать, чтобы выполнялось равенство математических ожиданий и корреляционных функций и, как.следствие, дисперсий с реальными процессами: 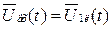, , 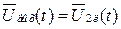, 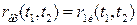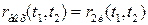(см. рис. 9.7, г).

После замены нелинейного звена по методу статистической линеаризации математические ожидания и корреляционные функции входной и выходной фазовых переменных модели функционального блока оказываются связанными линейно через коэффициенты линеаризации :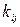

,

.

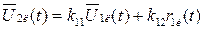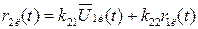С математической точки зрения метод статистической линеаризации эквивалентен разложению плотности вероятности реальной выходной переменной в ряд по моментам распределения входной переменной и усечения разложения линейными членами ряда.

Метод гармонической статистической линеаризации представляет развитие этого метода на функциональные блоки с колебательными процессами на входе и выходе. Однако нахождение коэффициентов линеаризации здесь значительно более затруднено, так как в ряде случаев, например при преобразовании частоты или детектировании, сигнал на выходе блока будет содержать составляющие, отсутствующие во входном сигнале. В этом случае для получения линейности звена, моделирующего функциональный блок, приходится вводить обратные связи либо включать ряд звеньев параллельно, причем каждое звено передает или генерирует свою статистическую составляющую выходной переменной. Для нахождения коэффициентов линеаризации здесь приходится использовать метод контурных интегралов.

Метод статистических эквивалентов обеспечивает большую скорость моделирования радиосистем при случайных воздействиях, однако он менее информативен, чем оба предыдущих метода, а модели будут адекватны реальным функциональным блокам только в сравнительно небольшом диапазоне изменения фазовых переменных.

Метод информационного параметра широко применяется для построения математических моделей систем и функциональных блоков следящего типа, в частности радиоустройств слежения за параметрами движения цели, систем радиоуправления и наведения, систем автоматического слежения за частотой и фазой, оптимальных демодуляторов сигналов с угловой модуляцией и в других случаях. В таких системах информационными параметрами, ради слежения за которыми и создается система, могут являться частота, фаза колебания, положение цели в пространстве и т.п., а измеренным параметром является оценка отслеживаемого параметра.

Сущность информационного метода заключается в замене реального входного воздействия в системе новым входным воздействием в виде информационного параметра, т.е. основной информационной характеристики системы. Этот подход позволяет моделировать только преобразование информации в системе и, следовательно, работать с низкочастотными моделями функциональных блоков, моделируя только преобразование информации в них. В результате появляется возможность увеличить дискрет имитационного времени, а значит, и ускорить процесс моделирования. Так, на рис. 9.9, а показана схема реальной системы фазовой автоподстройки частоты, находящейся под воздействием сигнала с переменной фазой 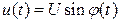и шума 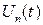,а на рис. 9.9, б приведена модель этой системы по методу информационного параметра, когда на вход системы подается сигнал рассогласования фаз между входными колебаниями и колебаниями с выхода управляемого генератора .

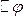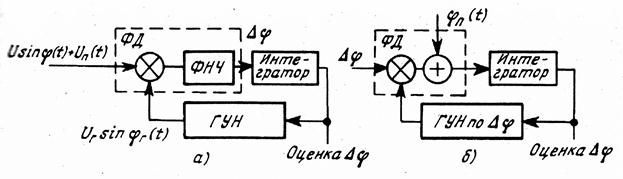
Рис. 9.9. Система ФАП и ее модель по методу информационного параметра

В настоящее время разработано достаточно большое число пакетов программ и специализированных систем для функционального моделирования больших систем набором функциональных блоков из области радиоэлектроники, из которых следует отметить ДИС, СИМУЛУ, МИК и др.