Если нижняя и верхняя цены игры в смешанных стратегиях совпадают, то их общее значение
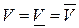
называется ценой игры в смешанных стратегиях, а стратегии 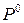 и для которых выполняются равенства
и для которых выполняются равенства
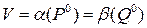
(и тогда это общее значение равно 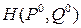 ), называются оптимальными смешанными стратегиями соответственно игроков А и В.
), называются оптимальными смешанными стратегиями соответственно игроков А и В.
Таким образом, оптимальные смешанные стратегии 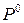 и
и 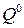 (которые, в частности, могут быть и чистыми) обладают тем свойством, что если один из игроков придерживается своей оптимальной стратегии, то противнику невыгодно отклоняться от своей оптимальной стратегии.
(которые, в частности, могут быть и чистыми) обладают тем свойством, что если один из игроков придерживается своей оптимальной стратегии, то противнику невыгодно отклоняться от своей оптимальной стратегии.
Нетрудно показать, что
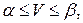
т. е. цена игры в смешанных стратегиях V не меньше нижней цены игры в чистых стратегиях а и не больше верхней цены игры в чистых стратегиях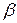 .
.
Полным решение игры в смешанных стратегиях называется совокупность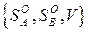 множеств оптимальных стратегий игроков и цены игры. Любая пара оптимальных стратегий
множеств оптимальных стратегий игроков и цены игры. Любая пара оптимальных стратегий  и цена игры V образуют частное решение в смешанных стратегиях.
и цена игры V образуют частное решение в смешанных стратегиях.
Основная теорема теории игр, сформулированная и доказанная фон Нейманом1, устанавливает существование решения любой конечной матричной игры.
Теорема 7.1 (основная теорема матричных игр фон Неймана). Любая матричная игра имеет решение в смешанных стратегиях, т. е. существуют цена игры в смешанных стратегиях V и оптимальные смешанные стратегии 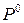 и
и 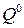 соответственно игроков А и В, т. е.
соответственно игроков А и В, т. е.
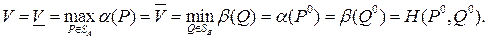
Теорема 7.2 (свойство равнозначности седловых точек). Если 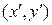 и
и 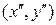 - седловые точки функции
- седловые точки функции 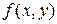 на декартовом произведении
на декартовом произведении 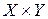 , то значения данной функции в этих точках совпадают:
, то значения данной функции в этих точках совпадают:
Теорема 7.3 (критерий существования седловой точки). Для того чтобы функция 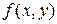 ,
, 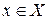 ,
, 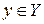 , имела седловую точку на декартовом произведении
, имела седловую точку на декартовом произведении 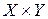 , необходимо и достаточно, чтобы существовали
, необходимо и достаточно, чтобы существовали
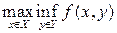 и
и 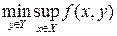
и выполнялось их равенство

Пример 7.1. Пусть 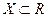 и
и 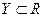 , т.е. х и у - скалярные переменные, и точки
, т.е. х и у - скалярные переменные, и точки 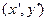 и
и 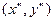 , которые графически изображаются двумя вершинами прямоугольника (см. рис. 7.1), являются седловыми точками функции
, которые графически изображаются двумя вершинами прямоугольника (см. рис. 7.1), являются седловыми точками функции 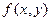 . Тогда по свойству взаимозаменяемости, сформулированному в теореме 9.3, остальные две вершины этого прямоугольника
. Тогда по свойству взаимозаменяемости, сформулированному в теореме 9.3, остальные две вершины этого прямоугольника 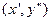 и
и 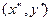 также являются седловыми. В связи с этим иногда свойство взаимозаменяемости седловых точек называют свойством "прямоугольности".
также являются седловыми. В связи с этим иногда свойство взаимозаменяемости седловых точек называют свойством "прямоугольности".
Если, в частности, 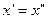 , то точки
, то точки 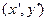 ,
, 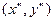 лежат на одной вертикали
лежат на одной вертикали 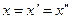 , а если
, а если 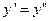 , то эти точки лежат на одной горизонтали
, то эти точки лежат на одной горизонтали  ; поэтому в этих случаях взаимозамена неравных координат этих точек приводит к паре тех же точек и прямоугольник вырождается в отрезок.
; поэтому в этих случаях взаимозамена неравных координат этих точек приводит к паре тех же точек и прямоугольник вырождается в отрезок.

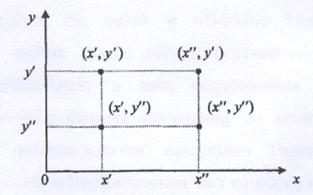
Рис. 7.1
Пример 9.3. Применяя критерий (теорема 9.4), определить, существует ли у функции

на декартовом квадрате [0,1]2 седловые точки.
Решение. Очевидно, что
 при любом
при любом 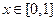 ,
,
и, следовательно,
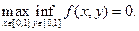
Также очевидно, что
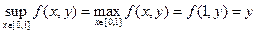 , при любом
, при любом 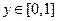
и потому
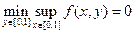 .
.
Итак, имеем
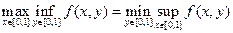
т.е. выполняются необходимые условия и потому на квадрате [0,1]2 существуют седловые точки.
 2014-02-02
2014-02-02 1514
1514
