Если матричная игра не имеет седловой точки, то решение игры затрудняется. В этих играх 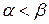 . Применение минимаксных стратегий в таких играх приводит к тому, что для каждого из игроков выигрыш не превышает
. Применение минимаксных стратегий в таких играх приводит к тому, что для каждого из игроков выигрыш не превышает 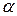 , а проигрыш – не меньше
, а проигрыш – не меньше 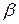 . Для каждого игрока возникает вопрос увеличения выигрыша (уменьшения проигрыша). Решение находят, применяя смешанные стратегии.
. Для каждого игрока возникает вопрос увеличения выигрыша (уменьшения проигрыша). Решение находят, применяя смешанные стратегии.
Смешанной стратегией первого (второго) игрока называется вектор
р = 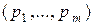 , где
, где 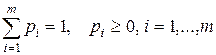 ,
,
q =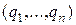 , где
, где 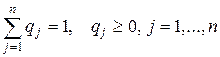 .
.
Вектор p (q) означает вероятность применения i -й чистой стратегии первым игроком (j -й чистой стратегии вторым игроком).
Поскольку игроки выбирают свои чистые стратегии случайно и независимо друг от друга, игра имеет случайный характер и случайной становится величина выигрыша (проигрыша). В таком случае средняя величина выигрыша (проигрыша) – математическое ожидание – является функцией от смешанных стратегий р, q:
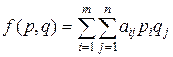 .
.
Функция f (p, q) называется платежной функцией игры.
Стратегии р* = 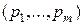 , q* =
, q* =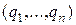 называются оптимальными, если для произвольных стратегий р =
называются оптимальными, если для произвольных стратегий р = 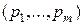 , q =
, q =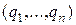 выполняется условие:
выполняется условие:
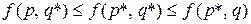 . (6.3)
. (6.3)
Использование в игре оптимальных смешанных стратегий обеспечивает первому игроку выигрыш, не меньший, чем при использовании им любой другой стратегии р; второму игроку – проигрыш, не больший, чем при использовании им любой другой стратегии q.
Совокупность оптимальных стратегий и цены игры составляет решение игры.
Значение платежной функции при оптимальных стратегиях определяет цену игры, т. е. 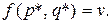
Теорема 6.2. В смешанных стратегиях любая конечная матричная игра имеет седловую точку.
Пусть имеем матричную игру и некоторые смешанные оптимальные стратегии р *, q * игроков А и В, обеспечивающие сумму выигрыша v. Вопрос поставим так: как проверить, что набор (р *, q *, v) является решением игры? Для этого нужно проверить справедливость неравенства (6.3) для любых смешанных стратегий, среди которых и будут стратегии р *, q *. Однако различных смешанных стратегий, среди которых и оптимальные, имеем бесчисленное множество. И в таком случае проверить справедливость неравенства (6.3) невозможно. Поэтому рассмотрим следующую теорему, которая позволит ответить на поставленный выше вопрос.
Теорема 6.3. Для того чтобы смешанные стратегии р*= 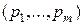 , q* =
, q* =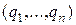 были оптимальными для игроков А и В в игре с матрицей
были оптимальными для игроков А и В в игре с матрицей 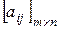 и выигрышем v, необходимо и достаточно выполнения неравенств:
и выигрышем v, необходимо и достаточно выполнения неравенств:
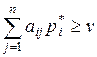 , (6.4)
, (6.4)
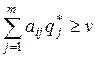 . (6.5)
. (6.5)
Доказательство. Пусть р *, q * – оптимальные смешанные стратегии. Докажем, что для них выполняются соотношения (6.4) и (6.5). Воспользуемся определением оптимальных смешанных стратегий, для которых выполняется соотношение (6.3). Неравенство (6.4) получается из соотношения (6.3), если записать его в развернутой форме, а именно:
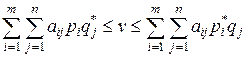 (6.6)
(6.6)
В правую часть соотношения (6.6) подставим вектор q = (0;...; 0; 1; 0;...; 0). Получим
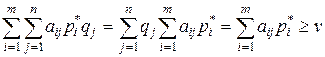 ,
,
т. е. оптимальная стратегия p * удовлетворяет неравенству (6.4).
Если вместо произвольного вектора р в левую часть соотношения (6.6) подставить вектор р * = (0;...; 0; 1; 0;...; 0), то аналогично можно показать, что и оптимальная стратегия q * удовлетворяет соотношению (6.5).
Итак, доказано условие необходимости, а именно: если стратегии р * и q * оптимальные, то они должны удовлетворять соотношениям (6.4) и (6.5).
Теперь докажем достаточность этого условия. Пусть выполняются неравенства (6.4), (6.5). Покажем, что р *, q * - оптимальные стратегии. Для этого нужно показать выполнимость соотношения (6.6). С учетом соотношения (6.4) преобразуем правую часть, а с учетом соотношения (6.5) – левую часть соотношения (6.6).
Пусть q =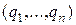 - произвольный вектор, тогда
- произвольный вектор, тогда
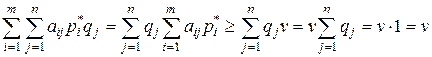 .
.
Преобразуя левую часть соотношения (6.6) для произвольного вектора р = 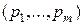 , получаем
, получаем
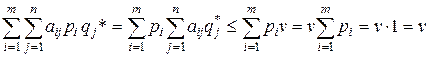 .
.
Итак, доказано, что если выполняются соотношения (6.4), (6.5), то выполняется и соотношение (6.6), т. е. смешанные стратегии р * и q * – оптимальные.
Таким образом, для проверки того, что набор (р *, q *, v) является решением матричной игры, достаточно проверить, удовлетворяют ли р *, q * неравенствам (6.4) и (6.5) и уравнениям
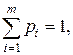
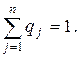
На основании данной теоремы можно сделать вывод: если игрок А применяет оптимальную смешанную стратегию р*, а игрок В – любую чистую стратегию, то выигрыш игрока А будет не меньше цены. игры.
Аналогично: если игрок В использует оптимальную смешанную стратегию q *, а игрок А – любую чистую стратегию, то проигрыш игрока В не превысит цены игры.
Чистые стратегии игрока, входящие в его оптимальную смешанную стратегию с вероятностями, отличными от нуля, называются активными стратегиями игрока. Рассмотрим теорему об активных стратегиях.
Теорема 6.4. Если один из игроков придерживается своей оптимальной смешанной стратегии, то его выигрыш остается неизменным и равным цене игры независимо от того, какую стратегию применяет другой игрок, если только тот не выходит за пределы своих активных стратегий.
На основании данной теоремы решение матричной игры можно упростить, выявив при этом доминирование одних стратегий над другими. Так, рассматривая стратегии игрока А, сравниваем соответствующие элементы строк s и t. Если все элементы s -й строки не меньше элементов
t -й строки, то выигрыш игрока А при стратегии As будет больше, чем при стратегии At. В этом случае стратегия As доминирует над стратегией At. Стратегию As называют доминирующей, а стратегию At – доминируемой.
Аналогично, поскольку игрок В заинтересован в минимизации проигрыша, доминирующим будет столбец с наименьшими элементами.
Если в матричной игре имеем строки (столбцы) с одними и теми же элементами, то строки (столбцы), а соответственно и стратегии игроков А и В, называются дублирующими.
В матричной игре доминируемые и дублирующие строки (столбцы) можно опускать, что не влияет на решение игры.
Теорема 6.5. Оптимальные смешанные стратегии р* и q* соответственно игроков А и В в матричной игре 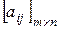 с ценой v будут оптимальными и в матричной игре
с ценой v будут оптимальными и в матричной игре 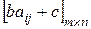 ценой v'=bv+c, где b>0.
ценой v'=bv+c, где b>0.
На основании теоремы 6.5 платежную матрицу, имеющую отрицательные числа, можно преобразовать в матрицу с положительными числами.
 2014-02-12
2014-02-12 1864
1864
