2014-02-02
989
Пусть игра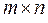 
не имеет оптимального решения в чистых стратегиях, т.е. седловая точка отсутствует 
.
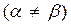Будем считать, что все элементы платежной матрицы неотрицательны (если это не так, то можно ко всем элементам матрицы добавить некоторое число L, переводящее платежи в область неотрицательных значений - при этом цена игры увеличится на L, а решение задачи не изменится). Таким образом, предполагаем, что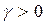 
.
Будем искать решение игры в смешанных стратегиях:
;.
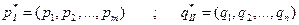Применение игроком I оптимальной смешанной стратегии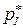 
гарантирует ему, независимо от поведения игрока II, выигрыш, не меньший цены игры 
.
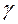Пусть игрок II применяет свою активную чистую j-ю стратегию, а игрок I - свою оптимальную стратегию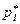 
. Тогда средний выигрыш игрока I будет равен
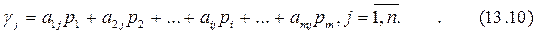
Учитывая, что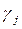 
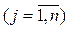не может быть меньше 
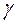, запишем условия:
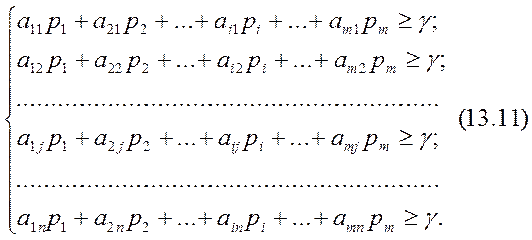
Разделив левую и правую части каждого из неравенств (10.3) на цену игры 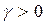, получим:
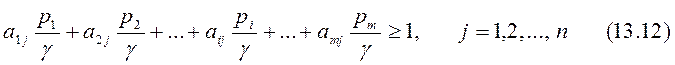
При использовании обозначений
неравенства (10.5) примут вид:
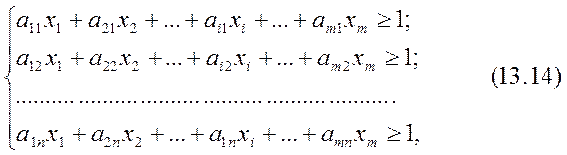
где, очевидно, все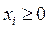 
, так как 
.
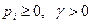Условие нормировки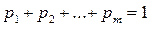 
с учетом определения (13.13) дает следующее соотношение
|
|
|
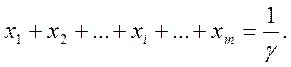
Учитывая, что игрок I стремится максимизировать 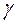, получаем линейную функцию
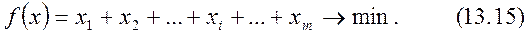
Таким образом, задача определения оптимальной смешанной стратегии свелась к стандартной задаче линейной оптимизации: найти неотрицательные значения переменных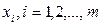 
, минимизирующие целевую функцию (13.15) и удовлетворяющие ограничениям (13.14).
Решение задачи линейной оптимизации позволяет найти цену игры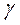 
и оптимальную стратегию
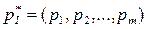первого игрока:
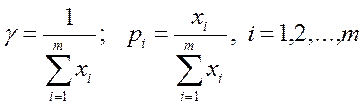
Аналогично можно показать, что оптимальная стратегия второго игрока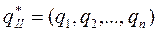 
определяется по формулам
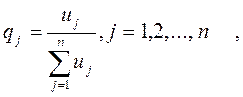
где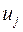 
- неотрицательные решения задачи линейной оптимизации, двойственной по отношению к исходной задаче:
,
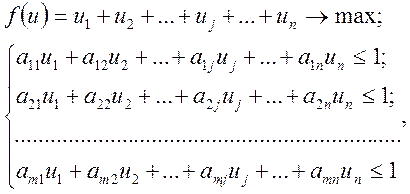а переменные
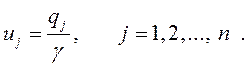
Таким образом, оптимальные стратегии первого и второго игроков могут быть найдены путем решения пары двойственных задач линейной оптимизации.
| Исходная задача | Двойственная задача |
| 
|
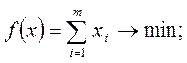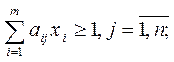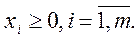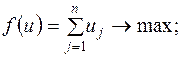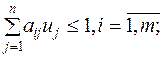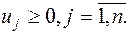Цена игры и вероятности применения стратегий игроками I и II равны:
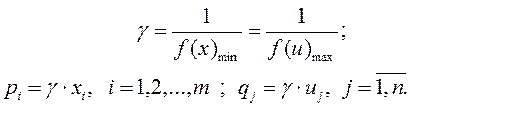
Проиллюстрируем вышесказанное на двух простых примерах.
