Дифференциальные уравнения простых элементов можно составить, используя закономерности протекающих в них физических явлений. Такими закономерностями могут быть: закон сохранения вещества (объекты регулирования уровня, давления), закон сохранения энергии (объекты регулирования температуры, тепловых нагрузок), закон равновесия электродвижущих сил, законы Ома, Кирхгофа и т.п. Математическое выражение основного закона, определяющего процесс, протекающий в элементе, и является исходным дифференциальным уравнением динамики элемента. Рассматривают уравнения статики и динамики элемента.
В качестве примера – бака с водой получим уравнение объекта регулирования уровня воды (рис. 2.5.).
| Рис. 2.5. Бак с водой как элемент САР |
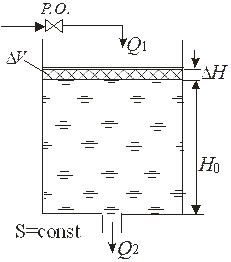
В бак поступает вода в количестве Q 1 [м3/с] и вытекает в количестве Q 2 [м3/с]. Площадь бака S [м2]; Н 0 – значение уровня в статическом режиме; D Н – отклонение уровня от установившегося значения Н 0.
Cтатический режим. В этом режиме приток воды в бак Q 1,0 равен ее расходу из бака Q 2.
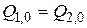 ;
; 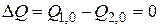 . (2.9)
. (2.9)
В этом режиме 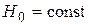 .
.
Динамический режим. В этом режиме приток воды Q 1 не равен ее расходу из бака Q 2 (Q 1 ¹ Q 2). Если приоткрыть регулирующий орган на притоке (Р.О.), то Q 1 будет больше Q 2 и объем воды будет увеличиваться на величину D V, что приведет к росту уровня воды на величину D Н.
Уравнение баланса расходов воды будет
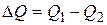 .
.
Возникший небаланс D Q [м3/с] равен скорости изменения объема воды в баке:
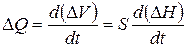 .
.
Тогда уравнение баланса в динамике примет вид
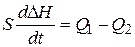 .
.
Приток Q 1 и расход воды Q 2 можно записать в виде
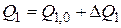 ;
; 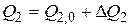 .
.
Тогда уравнение динамики примет вид
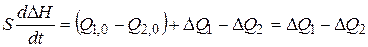 ,
,
так как 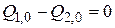 на основании (2.9). Получили уравнение в отклонениях от статического режима работы. В рассматриваемом баке расход Q 2 зависит от уровня воды в баке Н, т.е.
на основании (2.9). Получили уравнение в отклонениях от статического режима работы. В рассматриваемом баке расход Q 2 зависит от уровня воды в баке Н, т.е. 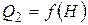 . При малых отклонениях от статического режима можно Q 2 линеаризовать:
. При малых отклонениях от статического режима можно Q 2 линеаризовать:
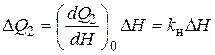 .
.
Тогда уравнение динамики бака примет вид
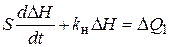 . (2.10)
. (2.10)
В теории линейных систем автоматического регулирования дифференциальные уравнения часто переводят в безразмерную форму. Это позволяет сравнивать динамические и статические характеристики элементов, которые имеют совершенно различные принципы действия и в которых протекают процессы разной физической природы.
Для перевода дифференциального уравнения в безразмерную форму отклонения входных и выходных величин относят к базовым значениям величин (максимальным, средним, заданным постоянным). Тогда входные и выходные величины элемента выражаются в долях от этих базовых значений.
Примем для уравнения (2.10) за базовое значение уровня заданное значение Н 0, а для изменения притока – его максимальное значение Q 1max при полностью открытом регулирующем органе.
Безразмерные величины: выходная – 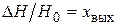 ; входная
; входная 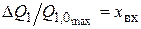 .
.
После подстановки этих значений в (2.10) получим
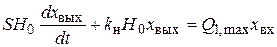 . (2.11)
. (2.11)
Запишем это уравнение в принятом в автоматике стандартном виде, когда коэффициент при свободном члене х вых в левой части уравнения равен единице. Тогда уравнение (2.11) примет вид
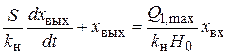 . (2.12)
. (2.12)
Введем обозначения: 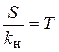 ;
; 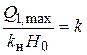 . Тогда имеем
. Тогда имеем
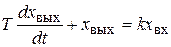 . (2.13)
. (2.13)
В этом уравнении коэффициент при производной Т имеет размерность времени и называется постоянной времени. Физический смысл постоянной времени выясняется конкретно для каждого элемента. Коэффициент k безразмерный и называется коэффициентом усиления, так как он показывает, во сколько раз выходная величина х вых отличается от входной х вх в статическом режиме работы.
Уравнение статики из (2.13) имеет вид
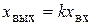 и
и 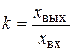 . (2.14)
. (2.14)
Коэффициент усиления k полностью характеризует статические свойства объекта.
Если последовательно соединить два бака с водой, то для изменения безразмерного уровня воды во втором баке можно получить
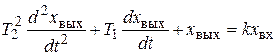 , (2.15)
, (2.15)
где Т 2 и Т 1 – постоянные времени; k – коэффициент усиления.
Решение уравнений (2.13) и (2.15) полностью определяет динамику элементов.
Линейные дифференциальные уравнения, используемые для описания динамики элементов и систем автоматического регулирования, можно решить классическим методом или путем применения преобразования Лапласа. Согласно классическому методу, решение линейного неоднородного уравнения, по которому определяют изменение величин х вых(t) во времени при заданном возмущении х вх(t) и известных начальных условиях, можно представить в виде суммы:
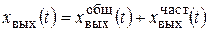 ,
,
где 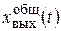 – общее решение однородного дифференциального уравнения;
– общее решение однородного дифференциального уравнения; 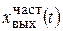 – частное решение неоднородного дифференциального уравнения (с учетом правой части).
– частное решение неоднородного дифференциального уравнения (с учетом правой части).
Поскольку общее решение однородного уравнения не зависит от правой части уравнения (2.13), (2.15) и характера изменения входного воздействия х вх(t), то составляющая 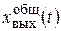 решения определяет свободное движение элемента и называется переходной (свободной) составляющей. Частное решение
решения определяет свободное движение элемента и называется переходной (свободной) составляющей. Частное решение 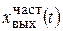 определяет вынужденное движение элемента, обусловленное действием х вх(t), и зависит как от параметров элемента (T, k), так и от закона изменения входного возмущения х вх(t). Частное решение
определяет вынужденное движение элемента, обусловленное действием х вх(t), и зависит как от параметров элемента (T, k), так и от закона изменения входного возмущения х вх(t). Частное решение 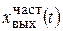 называется вынужденной составляющей и характеризует установившийся процесс в системе.
называется вынужденной составляющей и характеризует установившийся процесс в системе.
Решение линейных дифференциальных уравнений более высоких порядков классическим методом представляет собой более сложную задачу, поэтому в теории автоматического управления и регулирования переходят к алгебраическим уравнениям, записывая дифференциальные уравнения в символической (операторной) форме. Переход к этой форме осуществляют введением сокращенного условного обозначения операции дифференцирования:
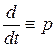 ;
; 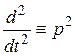 ; …;
; …; 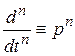 .
.
Тогда уравнения (2.13) и (2.15) в операторной форме будут иметь вид
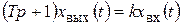 ; (2.16)
; (2.16)
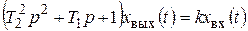 . (2.17)
. (2.17)
Обыкновенное дифференциальное уравнение с постоянными коэффициентами, описывающее динамические свойства линейной системы, имеющей одну входную х вх(t) и одну выходную величины х вых(t), имеет вид
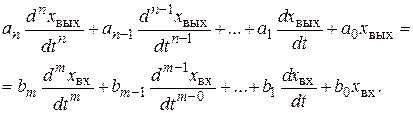 (2.18)
(2.18)
Уравнение в символической (операторной) форме будет
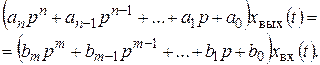 (2.19)
(2.19)
Многочлены от р степени n и m, находящиеся в левой и правой частях уравнения (2.19), называют дифференциальными операторами. Каждый такой оператор устанавливает соответствие между функцией времени и определенной совокупностью производных этой функции.
Многочлен правой части уравнения
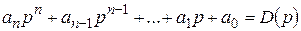 (2.20)
(2.20)
называют собственным оператором, а многочлен в левой части уравнения
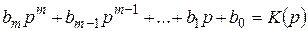 (2.21)
(2.21)
называют оператором воздействий.
Название собственный оператор обусловлено тем, что многочлен D (р) характеризует собственное движение элемента, то есть движение при отсутствии внешних воздействий.
У всех реальных элементов и систем порядок наивысшей производной во входном операторе (m) не может быть больше порядка наивысшей производной в собственном операторе (n), т.е. всегда m £ n. Если в процессе каких-либо формальных выкладок образуется уравнение, у которого m > n, то говорят, что это уравнение соответствует физически нереализуемой системе.
Уравнения элементов невысокого порядка принято записывать в стандартной форме, при которой коэффициент при выходной величине х вых(t) равен единице. Тогда коэффициент перед входной величиной х вх(t) в правой части уравнения становится равным передаточному коэффициенту, а коэффициенты при производных будут иметь размерность времени в степени, равной порядку соответствующей производной.
Например, имеем уравнение второго порядка
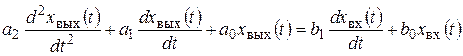 . (2.22)
. (2.22)
Тогда символическая (операторная) форма уравнения (2.22) имеет вид
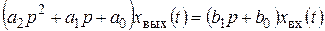 . (2.23)
. (2.23)
Путем деления всех членов уравнения (2.22) на коэффициент а 0 получим
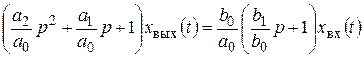 , (2.24)
, (2.24)
или
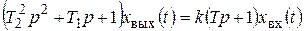 , (2.25)
, (2.25)
где 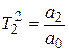 ;
; 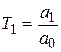 ;
; 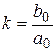 ;
; 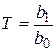 .
.
Коэффициенты Т, Т 1, Т 2 – постоянные времени, характеризующие динамические свойства элемента; k – коэффициент передачи элемента.
Строгий перевод дифференциальных уравнений в операторную форму осуществляется операционным методом, в основе которого лежит интегральное преобразование Лапласа.
Преобразование Лапласа состоит в том, что вместо функции времени х (t) используют функцию комплексной переменной 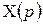 , где
, где 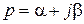 . Функция
. Функция 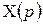 называется изображением функции х (t) по Лапласу, а функция х (t) называется оригиналом функции
называется изображением функции х (t) по Лапласу, а функция х (t) называется оригиналом функции 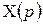 . Операция перехода от х (t) к
. Операция перехода от х (t) к 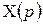 называется прямым односторонним преобразованием Лапласа и обозначается символом L:
называется прямым односторонним преобразованием Лапласа и обозначается символом L:
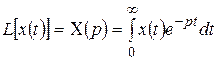 . (2.26)
. (2.26)
На основании (2.26) можно записать изображения по Лапласу функций х вых(t) и х вх(t):
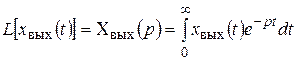 ,
,
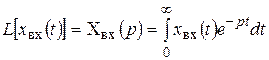 .
.
Преобразования Лапласа выполнимы лишь для таких функций времени, которые равны 0 при t < 0. Это условие обеспечивается обычно умножением функции х (t) на единичную ступенчатую функцию 1(t). С математической и физической точек зрения такой искусственный прием корректен, так как функции х (t) описывают процессы в автоматических системах, начинающиеся с некоторого момента времени, который всегда можно принять за начало отсчета.
Изображения простейших функций времени, наиболее часто используемых в расчетах автоматических систем, приведены в табл. 2.1.
Таблица 2.1
Изображение простейших функций по Лапласу
| Функция | x (t) | X(p)= L { x (t)} |
| Дельта-функция | d(t) | |
| Ступенчатая функция | 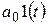 | 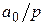 |
| Степенная функция | 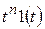 | 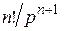 |
| Экспонента | 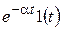 | 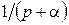 |
| Синусоида | 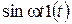 | 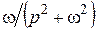 |
| Косинусоида | 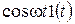 | 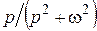 |
| Периодическая функция | 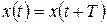 | 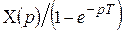 |
При анализе автоматических систем используют основные свойства преобразования Лапласа, приведенные в табл.2.2.
Наиболее важными свойствами преобразования Лапласа являются свойства, формулируемые в виде правил:
| при нулевых начальных условиях дифференцированию оригинала х (t)по переменной t соответствует умножение Х(р) на комплексную переменную р, а интегрированию оригинала соответствует деление Х(р) на р. |
На этих двух свойствах основан операционный метод решения дифференциальных уравнений, который заключается в следующем. Исходное дифференциальное уравнение (или интегродифференциальное), записанное относительно искомой выходной функции х вых(t), заменяют алгебраическим уравнением относительно изображения Хвых(р).
Таблица 2.2
Основные свойства преобразования Лапласа
| Наименование | Оригинал | Изображение |
| Линейность | 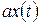 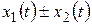 | 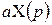 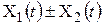 |
| Правило дифференцирования (при нулевых начальных условиях) | 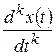 | 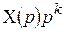 |
| Правило интегрирования (при нулевых начальных условиях) | 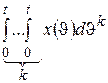 | 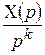 |
| Смещение аргумента оригинала (теорема запаздывания) | 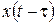 | 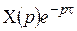 |
| Теорема о начальном значении оригинала | 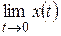 | 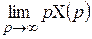 |
| Теорема о конечном значении оригинала | 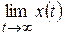 | 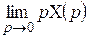 |
Решая алгебраическое уравнение при заданном Хвх(р), находят изображение Хвых(р) и, наконец, по изображению Хвых(р) определяют х вых(t) обратным преобразованием. Этот переход от изображений Х(р) к оригиналам х (t)может быть осуществлен при помощи таблиц, имеющихся в справочниках по операционному исчислению.
Применим преобразование Лапласа к дифференциальному уравнению (2.22), полагая, что до приложения внешнего воздействия х вх(t) система находилась в покое и все начальные условия равны нулю. Используя свойство линейности и правило дифференцирования (см. табл. 2.2), получим алгебраическое уравнение в изображениях:
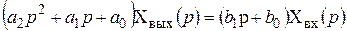 . (2.27)
. (2.27)
Сравнивая уравнения (2.27) с уравнением (2.23), записанным в символической форме, можно увидеть, что они полностью совпадают по структуре. Различие уравнений лишь в значении символа р: в уравнении (2.23) он обозначает операцию дифференцирования, а в уравнении (2.27) – комплексную переменную. Следовательно, для перехода от дифференциального уравнения к операторному (алгебраическому относительно изображений при нулевых начальных условиях) необходимо символы дифференцирования оригиналов функций 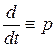 ;
; 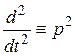 ; …;
; …; 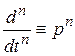 заменить соответственно символами р; р 2; …; р n, а функции х (t) – их изображением Х(р).
заменить соответственно символами р; р 2; …; р n, а функции х (t) – их изображением Х(р).
Из уравнения (2.27) следует его запись в общем виде:
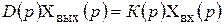 , (2.28)
, (2.28)
где 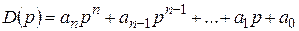 – собственный оператор;
– собственный оператор; 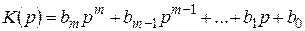 – оператор воздействий.
– оператор воздействий.
Широкое распространение операционного метода в теории автоматического управления обусловлено тем, что с его помощью определяют так называемую передаточную функцию, которая является самой компактной формой описания динамических свойств элементов и систем.
Передаточной функцией W (р) называют отношение изображения по Лапласу выходной величины к изображению по Лапласу входной величины при нулевых начальных условиях:
 . (2.29)
. (2.29)
Для системы, описываемой уравнением (2.28), передаточная функция W (р) равна
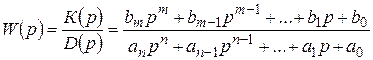 , (2.30)
, (2.30)
т.е. передаточная функция равна отношению оператора воздействий К (р) к собственному оператору D (р).
Как следует из (2.29) и (2.30), передаточная функция представляет собой некоторый динамический оператор, характеризующий прохождение сигнала через линейный элемент (рис.2.6).
| Рис. 2.6. Схема для определения передаточной функции |

Зная передаточную функцию элемента, сложного соединения элементов или системы, можно определить изображение выходной величины по известному изображению входной:
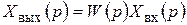 . (2.31)
. (2.31)
Из сопоставления уравнений (2.31) и (2.30) следует простое правило получения передаточной функции элемента или системы по их дифференциальному уравнению:
1. Производные в левой и правой частях дифференциального уравнения заменяют величиной р в степени, равной порядку производной.
2. Полученный таким образом полином правой части уравнения есть числитель передаточной функции, а полином левой части – ее знаменатель.
Приравняв полином знаменателя передаточной функции к нулю, получим характеристическое уравнение элемента или системы:
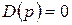 . (2.32)
. (2.32)
Корни этого уравнения называются полюсами передаточной функции.
Тогда процедура решения дифференциального уравнения с использованием преобразования Лапласа состоит в следующем:
1. По заданному входному воздействию х вх(t) с помощью таблиц соответствия находят изображение Х вх(р).
2. По дифференциальному уравнению составляют передаточную функцию W (р).
3. Находят изображения выходной величины Х вых(р) как произведение 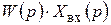 .
.
4. Определяют оригинал выходной величины х вых(t), соответствующий Х вых(р), по таблицам обратных преобразований, приведенных в справочниках по операционному исчислению.
Передаточные функции элементов системы согласно уравнениям (2.16), (2.17) и (2.25) соответственно будут
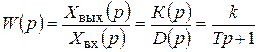 ,
,
где 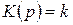 ;
; 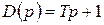 ;
;
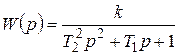 ,
,
где 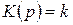 ;
; 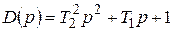 ;
;
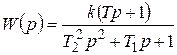 ,
,
где 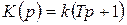 ;
; 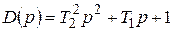 .
.
Таким образом, передаточная функция элемента (системы) полностью определяет его (ее) динамические свойства, и начальная задача расчета САР сводится к определению ее передаточной функции. Для упрощения задачи нахождения передаточной функции системы целесообразно систему предварительно представить в виде структурной схемы с элементарными, желательно типовыми в динамическом отношении, элементами (звеньями).
Определив передаточные функции элементов (звеньев) автоматической системы регулирования, можно найти передаточную функцию системы в целом. Систему любой сложности можно всегда рассматривать как совокупность различных видов соединений простейших элементов: последовательного, параллельного и соединения с обратной связью.
Последовательное соединение элементов (звеньев). При последовательном соединении элементов выходная величина предыдущего элемента является входной величиной последующего (рис. 2.7).

Рис. 2.7. Последовательное соединение элементов
Изображение 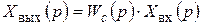 , где
, где 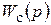 – передаточная функция последовательного соединения. Имеем
– передаточная функция последовательного соединения. Имеем
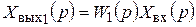 ;
;
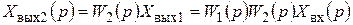 ;
;
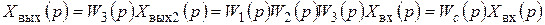 .
.
Следовательно, 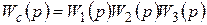 .
.
| Передаточная функция системы последовательно соединенных элементов (звеньев) равна произведению передаточных функций отдельных элементов: |
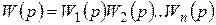 . (2.33)
. (2.33)
Если все элементы линейны и характеризуются только коэффициентами усиления k 1, k 2 и k 3 (рис. 2.6), то
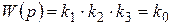 ,
,
т.е. общий коэффициент усиления последовательного соединения элементов равен произведению коэффициентов усиления всех элементов. Размерность общего коэффициента усиления k 0 равна произведению размерностей коэффициентов k 1, k 2, k 3.
Параллельное соединение элементов. Параллельным соединением называют соединение, в котором на вход всех элементов подается одно и то же воздействие х вх(t), а их выходные величины (с соответствующим знаками) суммируются (рис. 2.8).
| Рис. 2.8. Параллельное соединение элементов |
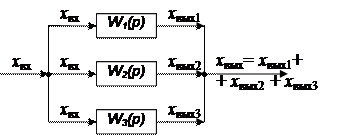
Для соединения из трех элементов имеем передаточную функцию
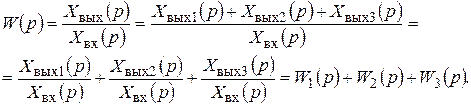 (2.34)
(2.34)
| Следовательно, передаточная функция параллельного соединения элементов равна сумме передаточных функций отдельных элементов: |
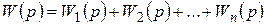 .
.
Если элементы линейны и характеризуются только коэффициентами усиления k 1, k 2, k 3, то
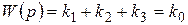 .
.
Следовательно, общий коэффициент усиления параллельного соединения элементов равен сумме коэффициентов усиления элементов. Это возможно только в том случае, когда их размерности одинаковы. Поэтому коэффициенты усиления всех параллельно включенных элементов должны иметь одинаковую размерность.
Последовательное соединение элементов с обратной связью. В таких соединениях выходная величина какого-либо элемента подается на его вход или на вход предыдущих элементов. Такая подача выходного сигнала называется обратной связью (рис.2.8).
 | 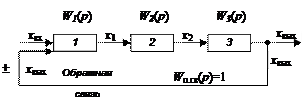 |
| А | б |
| Рис. 2.8. Последовательное соединение элементов с обратной связью: а – с неединичной обратной связью; б – с единичной обратной связью |
На рис. 2.8 представлены схемы с неединичной обратной связью (рис.2.8, а), где в обратную связь включен элемент 4 с передаточной функцией W о.св.(р), и с единичной обратной связью (рис.2.8, б), т.е. прямое соединение, передаточная функция которого W о.св.(р)=1. Сигнал обратной связи может быть подан на вход элемента 1 со знаком «+» или «–». Знак «+» говорит о том, что общий входной сигнал на входе элемента 1 будет представлен суммой основного сигнала х вх и сигнала обратной связи х о.св, т. е. входной сигнал на входе элемента 1 усиливается (положительная обратная связь), а при знаке «–» – сигнал обратной связи х о.св. будет вычитаться из основного входного сигнала х вх (х вх – х о.св), т.е. входной сигнал элемента 1 будет ослабляться (отрицательная обратная связь).
Изображение выходной величины обратной связи (элемента 4) равно
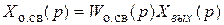 . (2.35)
. (2.35)
Можно определить передаточную функцию замкнутой системы с обратной связью (рис.2.8 а), разорвав обратную связь и заменив х вх сигналом 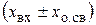 . Тогда в разомкнутой системе с элементами 1, 2, 3 будут происходить те же изменения, что и в замкнутой системе. Передаточная функция разомкнутой системы равна
. Тогда в разомкнутой системе с элементами 1, 2, 3 будут происходить те же изменения, что и в замкнутой системе. Передаточная функция разомкнутой системы равна 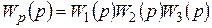 . Тогда имеем
. Тогда имеем
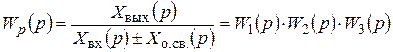 . (2.36)
. (2.36)
Передаточная функция замкнутой системы по определению равна
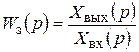 . (2.37)
. (2.37)
Ее можно определить из (2.36)
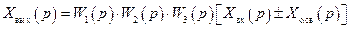 . (2.38)
. (2.38)
Из (2.38) следует передаточная функция замкнутой системы
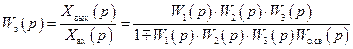 . (2.39)
. (2.39)
При единичной обратной связи 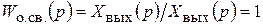 и передаточная функция замкнутой системы равна
и передаточная функция замкнутой системы равна
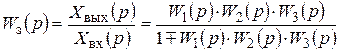 . (2.40)
. (2.40)
Знак «–» говорит о том, что использована положительная обратная связь, а знак «+» – отрицательная обратная связь.
В системах регулирования используется всегда отрицательная обратная связь. Тогда
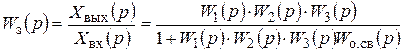 . (2.41)
. (2.41)
Положительная обратная связь обычно используется в усилителях различного типа, в которых выходной сигнал х вых(t) будет с течением времени возрастать.
В формуле (2.41) в числителе стоит передаточная функция прямой цепи элементов
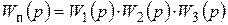 , (2.42)
, (2.42)
охваченных обратной связью.
Тогда можно дать общую формулировку:
| Передаточная функция элементов, охваченных отрицательной обратной связью, равна передаточной функции прямой цепи, разделенной на единицу, плюс произведение передаточных функций прямой цепи и обратной связи. |
Формула (2.41) выражает одно из фундаментальных правил теории автоматического управления.
Если система (рис. 2.8, а) состоит из линейных элементов с передаточными функциями: 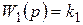 ;
; 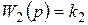 ;
; 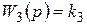 ;
; 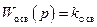 , то коэффициент усиления прямой цепи будет
, то коэффициент усиления прямой цепи будет 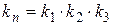 , а передаточная функция замкнутой системы будет равна
, а передаточная функция замкнутой системы будет равна
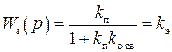 , (2.43)
, (2.43)
где k э – эквивалентный коэффициент усиления (коэффициент передачи) соединения с обратной связью. Его размерность равна размерности коэффициента усиления прямой цепи k п. Произведение 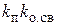 всегда безразмерно.
всегда безразмерно.
Из выражения (2.43) следует, что отрицательная обратная связь уменьшает эквивалентный коэффициент k э, а положительная (в знаменателе появится знак “-”) увеличивает. Если при положительной обратной связи произведение 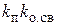 =1, то коэффициент k э возрастает до бесконечности (систем устойчива), а если
=1, то коэффициент k э возрастает до бесконечности (систем устойчива), а если 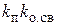 >1, то положительная обратная связь преобразует соединение в инвертор (элемент, изменяющий знак входного сигнала) с эквивалентным коэффициентом k э.
>1, то положительная обратная связь преобразует соединение в инвертор (элемент, изменяющий знак входного сигнала) с эквивалентным коэффициентом k э.
Отрицательная обратная связь уменьшает отклонения выходной величины, возникающие в исходной прямой цепи из-за нестабильности коэффициента k п, в (1+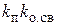 ) раз. Нестабильность самого коэффициента
) раз. Нестабильность самого коэффициента 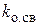 обратной связью не компенсируется.
обратной связью не компенсируется.
При достаточно большом значении произведения 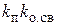 эквивалентный коэффициент k э практически не зависит от коэффициента k п. Если
эквивалентный коэффициент k э практически не зависит от коэффициента k п. Если 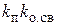 >>1, то
>>1, то
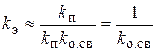 . (2.44)
. (2.44)
Это свойство широко используется при конструировании высокостабильных элементов, у которых изменяются коэффициенты усиления.
Таким образом, отрицательная обратная связь всегда уменьшает проявление нестабильности параметров линейных элементов и оказывает стабилизирующее действие на передаточные свойства прямой цепи.
Из рассмотрения одномерной системы автоматического регулирования (рис. 2.9) следует, на основании формулы (2.41), передаточная функция системы по каналу регулирующего воздействия m
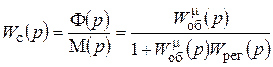 , (2.45)
, (2.45)
где М(р) и Ф(р) – изображения по Лапласу входной m(t) и выходной j(t) величин системы; 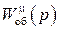 , W рег(р) – передаточные функции объекта регулирования и регулятора.
, W рег(р) – передаточные функции объекта регулирования и регулятора.
| Рис. 2.9. Структурная схема системы автоматического регулирования (САР) |

Регулятор является обратной связью по отношению к объекту регулирования, поэтому его называют главной отрицательной обратной связью. Для получения уравнения и передаточной функции системы регулирования необходимо знать свойства объекта регулирования (его передаточную функцию) и свойства регулятора (передаточные функции используемых законов регулирования).
Передаточные функции сложных систем. При получении передаточной функции сложных систем с множеством элементов (звеньев) и различными связями между ними основной подход к решению задачи заключается к сведению сложной структурной многоконтурной схемы к одноконтурной схеме путем замены элементов, охваченных различными связями, укрупненными эквивалентными элементами и устранению перекрестных связей в системе.
Значительно проще задача решается для систем, не имеющих перекрестных связей (рис.2.10).
| Рис. 2.10. Сложная система без перекрестных связей: I, II – элементы, охваченные связями | 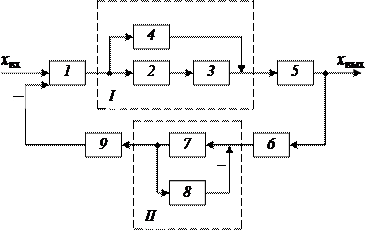 |
На рис. 2.10 сложный элемент I представляет собой последовательное соединение элементов 2 и 3, которые охвачены параллельно элементом 4. Передаточная функция элемента I
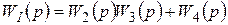 .
.
Сложный элемент II представляет элемент 7, охваченный отрицательной обратной связью, в которую включен элемент 8. Передаточная функция сложного элемента II
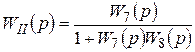 .
.
Тогда схема системы, представленной на рис.2.10, приводится к последовательному соединению элементов 1, I, 5, охваченных отрицательной обратной связью, состоящей из элементов 6, II, 9, и передаточная функция системы будет
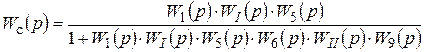 .
.
Сложнее определить передаточную функцию для системы с перекрестными связями. Тогда задача решается с использованием правил эквивалентного преобразования структурных схем, которые в основном сводятся к следующему (табл. 2.3):
Таблица 2.3
Правила структурных преобразований
| № п/п | Операция | Исходная схема | Преобразованная схема |
| Перенос сумматора через элемент (звено) вперед |  |  | |
| Перенос сумматора через элемент (звено) назад | 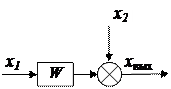 |  | |
| Перенос узла разветвления через элемент (звено) вперед |  |  | |
| Перенос узла разветвления через элемент (звено) назад |  |  | |
| Перестановка узлов разветвления | 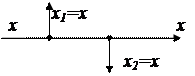 | 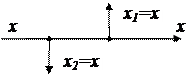 | |
| Перестановка сумматоров | 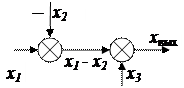 | 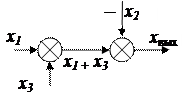 |
1. Перенос сумматора сигналов через элемент (звено) вперед производится добавлением элемента с этой же передаточной функцией (табл. 2.3, поз. 1).
2. Перенос сумматора через элемент (звено) назад производится добавлением элемента с передаточной функцией, обратной передаточной функции элемента (табл. 2.3, поз.2).
3. Перенос узла разветвления сигнала через элемент (звено) вперед производится добавлением элемента с передаточной функцией, обратной передаточной функции элемента (табл.2.3, поз.3).
4. Перенос узла разветвления через элемент (звено) назад производится добавлением элемента с такой же передаточной функцией (табл. 2.3, поз.4).
Можно переставлять узлы разветвления и сумматоры согласно схемам (табл. 2.3, поз.5 и 6).
Пользуясь приведенными выше правилами, можно любую сложную многоконтурную систему свести к простой одноконтурной.
Например, имеем многоконтурную систему с перекрещивающимися связями (рис.2.11,а). Пользуясь правилом 3 (см. табл. 2.3), можно перенести узел разветвления с входа элемента W 3 на его выход, добавив одновременно перед звеном W 6 обратную передаточную функцию 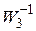 . Тогда получим схему – рис.2.11,б.
. Тогда получим схему – рис.2.11,б.
Согласно правилу 1 (см. табл.2.3) можно перенести сумматор А с входа элемента W 2 на его выход, включив последовательно с элементом W 5 элемент W 2 и поменяв по правилу 6 сумматоры А и В местами. Тогда получим одноконтурную схему (рис. 2.12), из которой определим передаточную функцию системы.
|
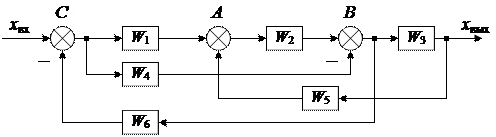
|
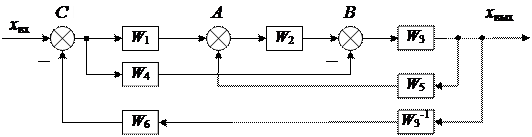
Рис. 2.11. Структурная схема сложной системы с перекрещивающимися связями
Сложные соединения в этой схеме выделены штрихами (I и II). Их передаточные функции
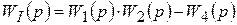 ;
;
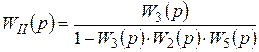 .
.
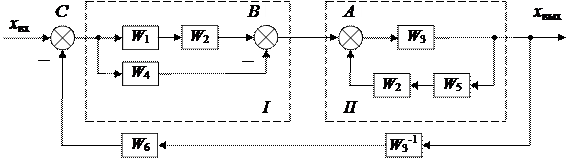
Рис. 2.12. Преобразованная схема системы
Передаточная функция системы
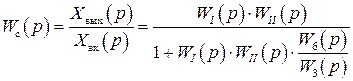 .
.
После подстановки WI (p) и WII (p) получим
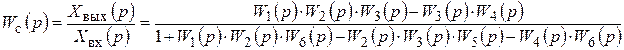 .
.
 2014-02-02
2014-02-02 6184
6184

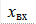 вх
вх