Конденсаторы. Электроемкость конденсатора. Электроемкость плоского конденсатора

Если двум изолированным друг от друга проводникам сообщить заряды q₁ и q₂, то между ними возникает некоторая разность потенциалов или напряжение U. Проще всего сообщить проводникам заряды, равные по модулю и противоположные по знаку. Если подключить проводники к разным полюсам источника тока, то источник тока перенесет заряд с одного проводника на другой, в результате один проводник будет иметь заряд + q, другой проводник будет иметь заряд – q.

Электроемкость системы из двух проводников - физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов 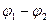между ними:

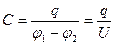. (10.4)

В системе СИ единица электроемкости называется фарад (Ф): .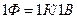

Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, – обкладками конденсатора.

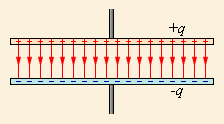Рис. 10.4.

Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами; однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. В целом ряде задач приближенно можно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками (рис. 10.4).

Каждая из заряженных пластин плоского конденсатора создает электрическое поле, модуль напряженности которого выражается соотношением:

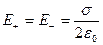, (10.5)

где 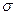- поверхностная плотность заряда пластин конденсатора, 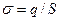, q – заряд, а S – площадь каждой пластины.

Согласно принципу суперпозиции, напряженность 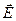поля, создаваемого обеими пластинами, равна сумме напряженносте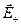й и 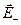полей каждой из пластин:

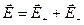
Внутри конденсатора векторы 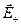и 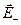параллельны; поэтому модуль напряженности суммарного поля равен:

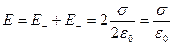
Вне пластин векторы 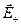и 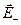направлены в разные стороны, и поэтому E = 0. Разность потенциалов 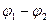между пластинами в однородном электрическом поле равна Ed, где d – расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:

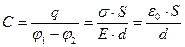. (10.6)

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:

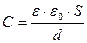. (10.7)