1.Построить каждую из прямых системы (7) и определить полуплоскость, соответствующую ограничениям (8).
2. Определить многоугольник решений.
3. Построить вектор градиента целевой функции 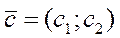 .
.
4. Построить прямую 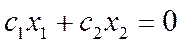 , проходящую через начало координат и перпендикулярную вектору
, проходящую через начало координат и перпендикулярную вектору 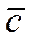 .
.
5. Следует передвигать данную прямую параллельно себе в направлении вектора 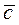 . Рассмотрим только линии пересекающие область допустимых решений (ОДР). Наиболее удаленные вершины ОДР соответствуют максимуму целевой функции. При поиске минимума следует передвигать прямую
. Рассмотрим только линии пересекающие область допустимых решений (ОДР). Наиболее удаленные вершины ОДР соответствуют максимуму целевой функции. При поиске минимума следует передвигать прямую 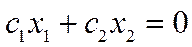 в направлении, противоположном
в направлении, противоположном 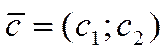 .
.
6. Определить координаты точек экстремума и значение целевой функции в этих точках.
В рассматриваемом примере 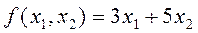 , поэтому
, поэтому 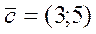 .
.
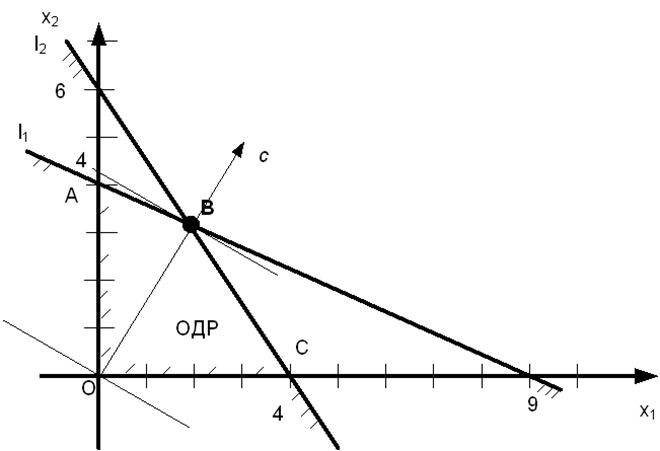
Максимум целевой функции достигается в точке 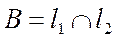 . Координаты точки В находятся из системы
. Координаты точки В находятся из системы
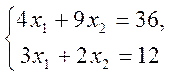
При решении таких систем можно воспользоваться правилом Крамера:
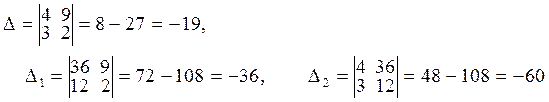
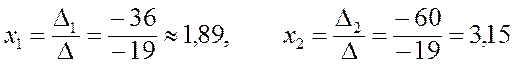 .
.
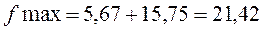 .
.
 2014-02-02
2014-02-02 1313
1313








