Графический метод решения задач линейного программирования с двумя переменными

Рассмотрим задачу линейного программирования с двумя переменными и ограничениями только в виде неравенств (стандартная форма задачи):

Ищем оптимальное значение целевой функции

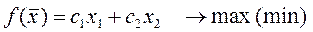(4)

с ограничениями

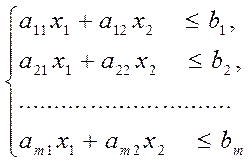, (5)

и условиями неотрицательности

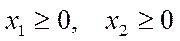. (6)

Решение задачи начинается с нахождения ОДР задачи, т.е. решения системы (5),(6).

Каждое из неравенств (5)-(6) геометрически определяет полуплоскость с граничными условиями

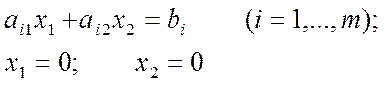(7)

Чтобы определить, какая именно полуплоскость, удовлетворяет неравенству

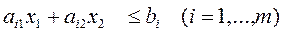(8)

достаточно проверить условие (8) для некоторой точки, например для начала координат О(0;0) (если ).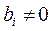

Рассмотрим пример задачи об использовании ресурсов:

Построим ОДР данной задачи.

Построим полуплоскость, определяемую неравенством:

.

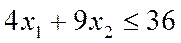Построим границу полуплоскости – прямую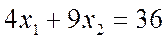

Прямая строится по двум точкам:

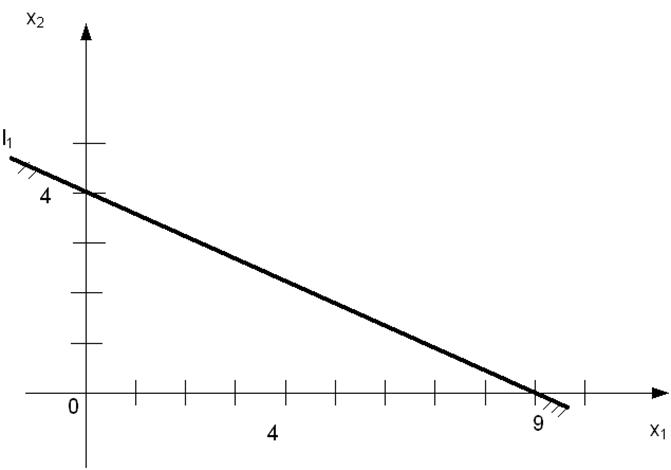
Поскольку начало координат О(0;0) удовлетворяет неравенству 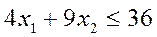: 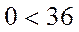, то выбрана нижняя полуплоскость.

Аналогично построим и полуплоскость .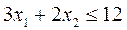

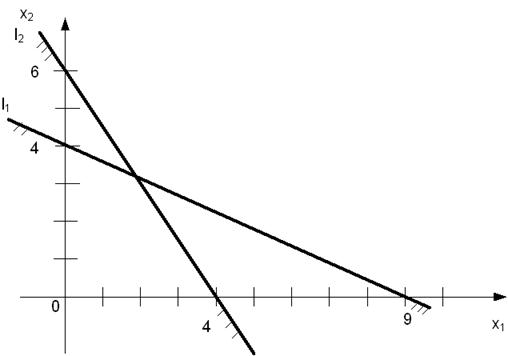
Условия неотрицательности выделяют только первую четверть плоскости.

Область пересечения всех полуплоскостей определяет область допустимых решений (ОДР) и является выпуклым четырехугольником ABCO:

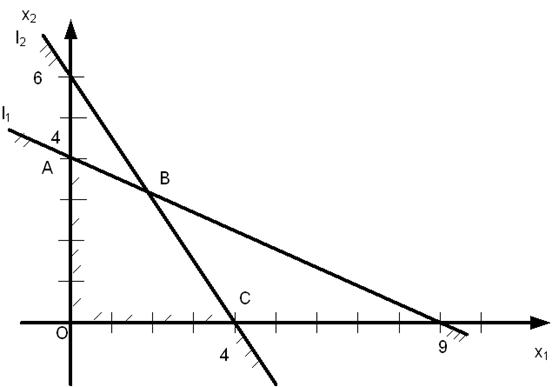
В общем случае, если система (5)-(6) имеет решение, то она выделяет выпуклую многоугольную область, которая называется многоугольником решений. Стороны этого многоугольника лежат на прямых (7).

Областью допустимых решений может быть:

− выпуклый многоугольник;

− выпуклая многоугольная неограниченная область.

Второй этап состоит в построении линий уровней целевой функции.

Линии уровней целевой функции (4) представляют собой семейство прямых

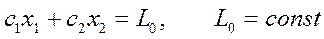, (9)

которые перпендикулярны вектору

.

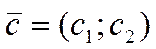Вектор 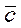указывает направление наискорейшего возрастания целевой функции, а противоположный вектор – направление убывания целевой функции.

В одной и той же системе координат изобразим область допустимых решений и линии уровня целевой функции.

Задача определения максимума (минимума) целевой функции 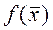сводится к нахождению в ОДР точки, через которую проходит прямая из семейства (9) и которая соответствует наибольшему (наименьшему) значению 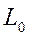. Возможны следующие случаи:

а)

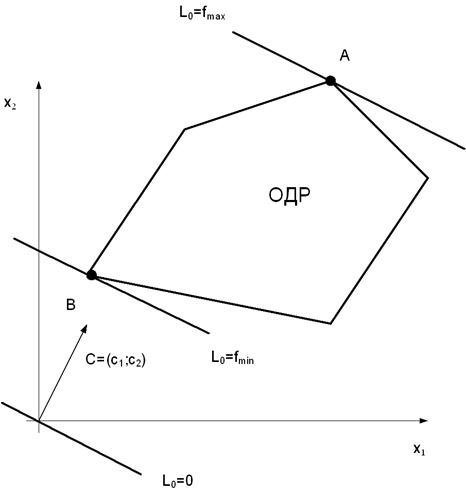
Максимум целевой функции достигается в точке A, минимум – в точке B.

б)

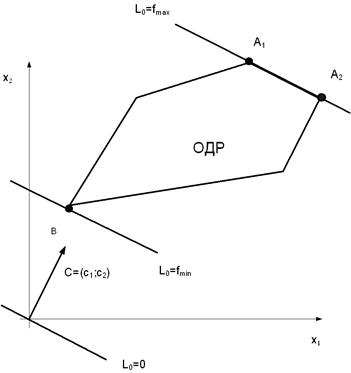
Максимум целевой функции достигается в любой точке отрезка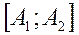, минимум – в точке B.

в)

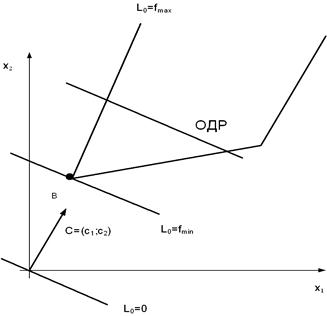
Максимум целевой функции недостижим, минимум – в точке B.