Основным методом решения задач линейного программирования является симплекс-метод. Геометрический смысл симплекс-метода состоит в последовательном переходе от одной вершины многогранника решений (называемой первоначальной вершиной) к соседней, в которой функция цели принимает лучшее (по крайней мере, не худшее) значение до тех пор, пока не будет найдено оптимальное решение – вершина, в которой достигается оптимальное значение функции цели.
Cимплекс-метод можно применять в том случае, когда задача программирования задана в каноническом виде. В дальнейшем, будем рассматривать задачи линейного программирования канонического вида, так как любая ЗЛП может быть сведена к решению канонической задачи.
Задача линейного программирования имеет канонический вид, если система ограничений задана множеством уравнений:
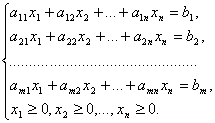
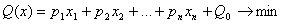
и каждое i -е уравнение содержит переменную 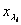 такую, что коэффициент перед ним в этом уравнении равен 1, а во всех других уравнениях равен 0. Если при этом
такую, что коэффициент перед ним в этом уравнении равен 1, а во всех других уравнениях равен 0. Если при этом 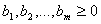 , то говорят о допустимом каноническом виде. Переменные
, то говорят о допустимом каноническом виде. Переменные 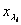 называют базисными, остальные – свободными.
называют базисными, остальные – свободными.
ЗЛП допустимого канонического вида может быть записана в допустимой симплекс-таблице следующего вида: левый крайний столбец содержит номера 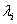 базисных переменных, верхняя строка – номера
базисных переменных, верхняя строка – номера 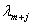 свободных переменных. В точке пересечения строки, соответствующей значению
свободных переменных. В точке пересечения строки, соответствующей значению 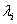 , и столбца, соответствующего
, и столбца, соответствующего 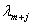 , стоит коэффициент
, стоит коэффициент 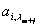 при свободной переменной в уравнении i, в котором выделена базисная переменная
при свободной переменной в уравнении i, в котором выделена базисная переменная 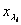 . Соответственно, справа записаны постоянные члены уравнений, внизу – коэффициенты целевой функции от свободных переменных, а в правом нижнем углу записано значение «-Q0».
. Соответственно, справа записаны постоянные члены уравнений, внизу – коэффициенты целевой функции от свободных переменных, а в правом нижнем углу записано значение «-Q0».
Симплекс-таблица
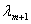 | … | 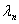 | ||
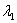 | 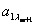 | … | 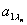 | 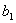 |
| … | … | … | … | |
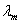 | 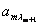 | … | 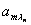 | 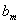 |
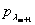 | … | 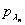 | 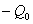 |
Допустимому каноническому виду ЗЛП или соответствующей допустимой симплекс-таблице сопоставляется точка  ,
, 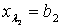 ,
, 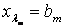 ,
, 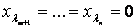 . Координаты этой точки удовлетворяют n линейно-независимым условиям ЗЛП: m уравнениям и n-m неравенствам
. Координаты этой точки удовлетворяют n линейно-независимым условиям ЗЛП: m уравнениям и n-m неравенствам 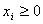 для свободных переменных. Эта точка является допустимым базисным решением и вершиной многогранника решений.
для свободных переменных. Эта точка является допустимым базисным решением и вершиной многогранника решений.
Допустимой симплекс-таблице соответствует точка минимума, если все коэффициенты целевой функции неотрицательны:
 , …,
, …, 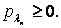
Тогда минимальное значение целевой функции равно 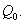
Если критерий не выполнен, то есть не все коэффициенты целевой функции неотрицательны, то следует перейти от одного допустимого решения к соседнему допустимому, то есть такому, в котором множества базисных и свободных переменных изменены на один элемент. Этот процесс называют симплекс-шагом или заменой базиса. Опишем последовательно его этапы.
1) Выбор разрешающего столбца: среди элементов последней строки таблицы выбирается любой 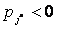 , и соответствующий столбец называется разрешающим. В качестве
, и соответствующий столбец называется разрешающим. В качестве 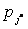 рекомендуется выбирать минимальное
рекомендуется выбирать минимальное 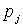 .
.
2) Выбор разрешающей строки: если 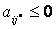 для всех элементов разрешающего столбца, то минимум не существует. Если это не так, то для всех положительных
для всех элементов разрешающего столбца, то минимум не существует. Если это не так, то для всех положительных 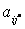 вычислим отношение
вычислим отношение 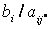 . Строка i, для которой отношение минимально, называется разрешающей строкой
. Строка i, для которой отношение минимально, называется разрешающей строкой 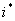 , общий элемент
, общий элемент 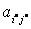 разрешающего столбца и разрешающей строки называется разрешающим элементом.
разрешающего столбца и разрешающей строки называется разрешающим элементом.
3) Замена базиса при помощи разрешающего элемента 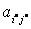 . Если w – какое-либо значение в таблице, то через
. Если w – какое-либо значение в таблице, то через 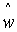 будем обозначать значение, стоящее в новой таблице на том же самом месте:
будем обозначать значение, стоящее в новой таблице на том же самом месте:
| а)номера переменных из разрешающей строки и разрешающего столбца меняются местами, | 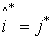 , , 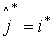 , , |
| номера других переменных остаются на месте | 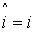 для всех для всех 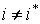 , , 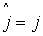 для всех для всех 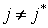 ; ; |
| б) разрешающий элемент заменяется на обратное значение: | 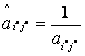 , , |
остальные элементы разрешающего столбца и разрешающей строки делят на разрешающий элемент со знаком «-» для элементов разрешающего столбца и со знаком «+» для элементов разрешающей строки, то есть
элементы разрешающего столбца 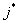 заменяются следующим образом: для всех заменяются следующим образом: для всех 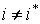 , , | 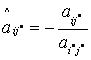 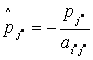 ; ; |
и элементы разрешающей строки 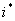 заменяются следующим образом: для всех заменяются следующим образом: для всех 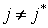 , , | 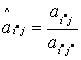 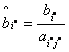 ; ; |
в) элементы симплекс-таблицы, не принадлежащие разрешающей строке и разрешающему столбцу, пересчитываются следующим образом - из элемента вычитается произведение соответствующих элементов из разрешающей строки и разрешающего столбца, деленное на разрешающий элемент:
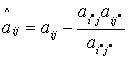 для всех
для всех 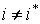 и
и 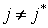 ,
,
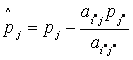 для всех
для всех 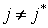 ,
,
 для всех
для всех 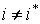 ,
,
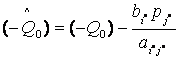 .
.
Всегда должно получаться 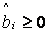 и
и 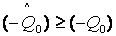 . Может случиться, что
. Может случиться, что 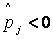 , хотя
, хотя 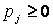 . После пересчета всех элементов симплекс-таблицы проверяется критерий минимальности - все коэффициенты целевой функции должны быть неотрицательны.
. После пересчета всех элементов симплекс-таблицы проверяется критерий минимальности - все коэффициенты целевой функции должны быть неотрицательны.
Отметим, что переменным, индекс которых стоит в верхней строке, в базисном решении приписывается значение 0; это свободные переменные. Каждая из переменных, индекс которых стоит в левом столбце, приравнивается к числу, записанному в правом столбце той же самой строки; это базисные переменные.
Каждой задаче линейного программирования можно сопоставить точно одну двойственную ей задачу линейного программирования.
 2014-02-02
2014-02-02 1584
1584
