Дифракция на идеальной кристаллической решетке. Дефекты кристаллической решетки

Для изучения взаимного расположения атомов используется дифракция микрочастиц: фотонов, электронов, нейтронов. Этими методами в основном получены данные о структуре кристаллов и молекул. При исследовании кристалла изучают распределение интенсивности дифракции частиц по разным направлениям, а затем по дифракционной картине делают выводы о типе элементарной ячейки кристалла и строении его базиса. Эти методы позволяют определять периоды кристаллической решетки с точностью до 4-5 знака и определять расположение атомов в базисе.

Для наблюдения дифракции необходимо чтобы длина волны де-Бройля дифрагирующих частиц была меньше периодов кристаллической решетки. Этому условию удовлетворяют рентгеновское и гамма- излучение, электроны при Е = 10-100 эВ и нейтроны при Е = 0,01- 0,1 эВ (тепловые нейтроны с энергией порядка kT). Наиболее просто осуществляется дифракция фотонов (рентгеновское излучение, гамма излучение), поэтому их используют чаще, чем дифракцию электронов, для наблюдения которой необходим высокий вакуум, или дифракцию нейтронов, для которой в качестве источника нейтронов нужен громоздкий ядерный реактор. Дифракция нейтронов и электронов очень похожа на дифракцию фотонов, поэтому рассмотрим применение дифракции фотонов для изучения структуры кристаллической решетки.

Закон Брэгга. Брэгг установил, что направление дифракционных пучков можно определить на основе простой модели, согласно которой падающие рентгеновские лучи зеркально отражаются от различных атомных плоскостей кристалла (рис. 1а). Дифрагированные пучки образуются в тех случаях, когда лучи заметно интерферируют, т.е. разность хода лучей равна целому числу длин волн:

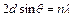. (1)

d – межплоскостное расстояние.

Формула (1) является следствием основного свойства кристалла – периодичности его структуры и не связана ни с химическим составом, ни с положением атомов в отражающих плоскостях. Одним из важных следствий формулы (1) является условие 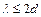– лишь при этом условии возможно брэгговское отражение. Чтобы выполнить условие Брэгга, подбирают экспериментально длины волн или углы скольжения. Например, пучок рентгеновских лучей или нейтронов направляется на неподвижный монокристаллический образец. В кристалле производится "отбор" лучей, при котором дифрагируют лучи, отвечающие условию (1). Данный метод удобен для определения симметрии кристалла и его ориентации. Он используется также для определения размеров искажений и дефектов кристалла.

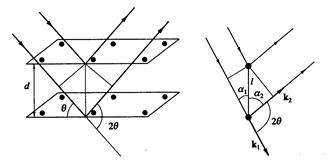Рис.1

а) б)

Условие Лауэ. Подход Лауэ отличается от подхода Брэгга тем, что в нем не выделяется никакой конкретный способ разбиения кристалла на атомные плоскости и не предполагается, что лучи зеркально отражаются. Лауэ считал, что кристалл состоит их тождественных объектов (атомов или ионов), размещенных в узлах 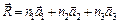решетки Бравэ. Каждый из них может рассеивать во всех направлениях падающее на него излучение (рис.1 б). Для интерференции необходимо, чтобы разность хода волн, переизлученных двумя атомами, находящимися на расстоянии l, составляла целое число длин волн:

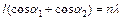или (2)

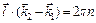, (3)

где 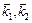– волновые векторы падающего и рассеянного луча. Сравнивая это выражение с (10) пункта 18 мы видим, что они совместимы, если 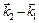является вектором обратной решетки. Т. е. интерференция будет эффективна, если изменение волнового вектора равно вектору обратной решетки.

Традиционная физика базируется на модели идеального кристалла. Но реальные кристаллы всегда имеют нарушения правильной структуры. Отклонения кристаллической решетки от правильной структуры называются дефектами. Дефекты могут вызвать появление внутренних напряжений в кристалле. Они влияют на спектры поглощения и излучения, изменяют электропроводность и теплопроводность кристалла, поляризуемость и магнитные свойства кристалла.

Классификация дефектов может производиться по числу измерений и по времени жизни. В первом случае различают точечные, линейные, поверхностные и объемные дефекты. Во втором случае различают короткоживущие и долгоживущие дефекты. Дефекты второго рода либо уничтожаются, просуществовав очень короткое время, либо мигрируют по кристаллу.

Рассмотрим различные точечные дефекты, изображенные на рис. 2.

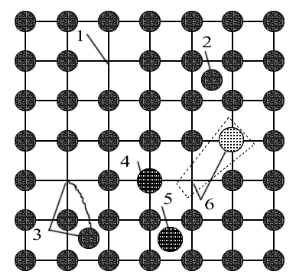Рис. 2.

1– вакансии – незаполненные узлы. Могут возникнуть при быстром росте кристалла или внешнем воздействии.

2– междоузельный атом. Атом размещается в промежутке между атомами.

3 – дефект по Френкелю. Одновременное появление вакансии и междоузельного атома. Такие спаренные дефекты обычно возникают в ионных кристаллах.

4 – примесный атом замещения. Один из атомов замещен атомом примеси.

5 – примесный атом внедрения. Примесный атом размещается в междоузлии.

6 – атом замещения большой валентности. Если атомы примеси, отличаются валентностью от атомов кристалла, то появляются вакансии, но кристалл в целом остается нейтральным.

При низких температурах плотность дефектов убывает экспоненциально и оказывается очень малой величиной при температурах ниже комнатной. Но и при низких температурах плотность дефектов может оказаться высокой, если кристалл, нагретый до высокой температуры, быстро охладить (закалить). Тогда плотность дефектов будет соответствовать высокой температуре.

С повышением температуры количество дефектов возрастает, и на их образование требуется дополнительная энергия. Поэтому в некоторых кристаллах вблизи температуры плавления, когда при нагреве намного увеличивается число дефектов, наблюдается эффект увеличения теплоемкости.

Точечные дефекты оказывают наиболее значительное влияние на скорость диффузии в кристаллах и на электропроводность в диэлектрических кристаллах. Электропроводность реальных кристаллов оказывается значительно выше электропроводности идеального кристалла вследствие наличия дефектов.

Вакансии и примеси влияют на цвет кристалла. Это связано с тем, что при отсутствии дефекта в определенном узле будет один спектр энергии колебаний электронов. При возникновении дефекта спектр энергии электронов изменяется и, следовательно, изменяется цвет. Например, примеси замещения – ионы хрома в кристаллах Al₂O₃ обеспечивают красную окраску кристалла рубина.

Линейные дефекты. Линейные дефекты называют дислокациями. Это дефекты, имеющие значительную протяженность в каком-либо направлении. Различают краевые (рис.3) и винтовые дислокации (рис.4).

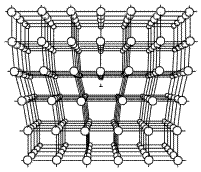
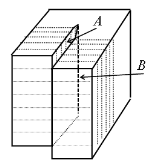
Рис.3. Рис. 4.

При краевой дислокации появляется лишняя часть плоскости или теряется часть плоскости. При этом на границе нарушения структуры возникают сильные деформации.

При винтовой дислокации атомы, расположенные с одной стороны от половинки плоскости А, остались на месте, а атомы с другой стороны смещены вниз на одно межплоскостное расстояние. На практике чаще встречаются смешанные дислокации, состоящие их краевых и винтовых. Линейные дислокации взаимодействуют друг с другом и с точечными дефектами. Считают, что отдельные точечные дефекты и их скопления закрепляют линейную дислокацию.

Поверхностные и объемные дефекты состоят из большого числа атомов. Поверхность кристалла сама является примером поверхностного дефекта, так как вблизи поверхности кристалла нарушается периодическое расположение атомов. Из-за этого поверхностный слой находится в напряженном состоянии и обладает некоторой поверхностной энергией, подобно тому, как и поверхность жидкости, обладает энергией поверхностного натяжения. Поверхностные дефекты встречаются и внутри кристалла. Это связано с тем, что большинство реальных кристаллов формируются одновременно из нескольких центров кристаллизации и поэтому состоят из зерен с близкой ориентацией кристаллических решеток. На границе раздела этих зерен неизбежно нарушается периодическое расположение атомов.

К объемным дефектам относят поры и трещины. Эти типы дефектов нежелательны для материала, так как искажают практически все его физические свойства.

20. Типы кристаллических твердых тел: металлы, диэлектрики. Полупроводники с собственной и примесной проводимостью.

Порядок в расположении узлов кристаллической решетки приводит к тому, что в твердых телах существует электрическое поле, которое является периодической функцией координат. Это поле существенно изменяет энергетический спектр электронов в твердом теле по сравнению с их спектром в изолированных атомах. В изолированных атомах электроны находятся на дискретных уровнях энергии (рис 1Б). В кристалле, состоящем из N атомов, из-за взаимодействия атомов одиночные уровни энергии электронов расщепляются в N близко расположенных уровней, которые образуют зону (рис. 1А).

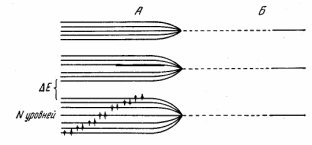
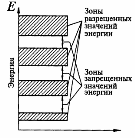
Рис.1 Рис. 2

На каждом уровне энергии в зоне может находиться по два электрона с противоположно ориентированными спинами. Соседние энергетические уровни в зоне отстоят друг от друга примерно на расстоянии 1/N эВ. Разрешенные зоны разделены запрещенными зонами. С увеличением энергии ширина разрешенных зон увеличивается, а запрещенных – уменьшается (рис.2).

Различия в электрических свойствах между металлами, диэлектриками и полупроводниками объясняют, используя представление о зонах.

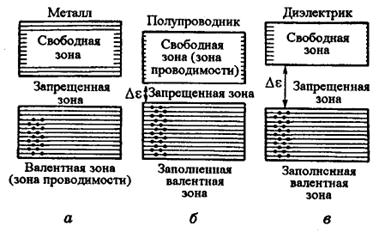Рис. 3

Типичными представителями проводников являются металлы первой группы периодической системы Менделеева, например, натрий. Его электронная конфигурация 1s²2s²2p⁶3s¹. Это одновалентный элемент, он имеет две полностью заполненные оболочки (K-, L-оболочку) и на его внешней оболочке находится только один электрон. В кристалле натрия двум полностью заполненным оболочкам изолированного атома соответствуют полностью заполненные зоны, а внешние электроны атомов натрия заполняют половину уровней разрешенной зоны. Такая зона называется зоной проводимости, так как находящиеся в ней электроны участвуют в создании тока. Таким образом, если разрешенная зона не полностью занята электронами, то кристалл всегда будет проводником.

Для элементов второй группы периодической системы Менделеева соседние разрешенные зоны могут пересекаться. При этом образуется широкая зона, заполненная электронами частично, такая зона также является зоной проводимости и такие кристаллы – проводниками.

В диэлектриках разрешенные зоны не перекрываются, запрещенные зоны широкие, поэтому электроны из заполненных зон не могут перейти в вышележащие свободные разрешенные зоны. Зона, полностью заполненная электронами, называется валентной, а находящаяся над ней пустая разрешенная зона – зоной проводимости. Примером диэлектрика является поваренная соль.

В полупроводниках при Т®0 электроны заполняют зоны так же, как в диэлектриках. Поэтому полупроводники при Т®0 электрический ток не проводят. Но ширина запрещенных зон у полупроводников меньше, чем у диэлектриков, поэтому при повышении температуры часть электронов из валентной зоны переходит в зону проводимости. На месте ушедших электронов в валентной зоне образуются дырки. Дырка ведет себя как положительный заряд, равный по величине заряду электрона. Проводимость полупроводника, обусловленная наличием дырок в валентной зоне и электронов в зоне проводимости называется собственной проводимостью.

На практике особенно большое значение имеют полупроводники, проводимость которых обусловлена примесями.

Рассмотрим два случая.

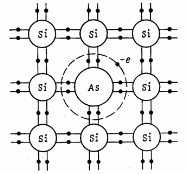
1) Пусть в кристалл кремния введена примесь мышьяка. Кремний четырехва лентный элемент, а мышьяк – пятивалентный. В решетке кремния 4 валентных электрона кремния образуют ковалентную связь с 4 валентными электронами мышьяка. Пятый электрон мышьяка, не принимающий участия в ковалентной связи, слабо связан с мышьяком. При низких температурах он находится около мышьяка, а при повышении температуры может свободно перемещаться по кристаллу. Доминирующую роль в проводимости будут играть электроны. Такие полупроводники называют полупроводниками n -типа, а примесь, дающую электроны – донорной.

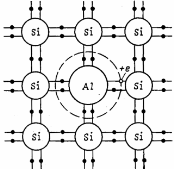
2) Пусть в кристалл кремния введена примесь алюминия. Алюминий – трехвалентный элемент. Три электрона алюминия образуют ковалентные связи с тремя электронами соседних атомов кремния, а одна связь соседнего кремния будет не завершена. В незаполненную связь около алюминия будет захвачен электрон от соседнего кремния. При этом будут образовываться положительные дырки, которые будут перемещаться по кристаллу. Примеси, захватывающие электроны, называются акцепторными, полупроводник с акцепторной примесью называется полупроводником p -типа.

Полупроводник, имеющий примеси, называется примесным. Проводимость, обусловленная примесями – примесной проводимостью. Наличие примесей в кристалле вызывает появление дополнительных уровней энергии, которые располагаются в запрещенной зоне. При этом уровень донорной примеси располагается ближе к зоне проводимости, а уровень акцепторной примеси располагается ближе к валентной зоне.

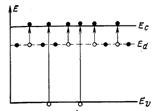Рис. 4 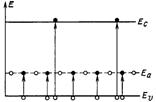Рис. 5

На рис.4 и 5 черные кружки – электроны, белые – дырки. На рис. 4 электроны с донорного уровня поступают в зону проводимости. На их месте остаются дырки. Это механизм примесной проводимости. Кроме того, электроны могут перейти из валентной зоны в зону проводимости. Это механизм собственной проводимости. На рис. 5 акцепторный уровень захватывает электроны из валентной зоны. На месте ушедших электронов в валентной зоне образуются дырки. Это механизм примесной проводимости. Как и в случае рис. 4, на рис.5 изображен еще механизм собственной проводимости.