Геометрия кристаллической решетки. Индексы Миллера. Обратная решетка

В идеальном кристалле центры атомов образуют периодическую структуру, называемую кристаллической решеткой. Точки, в которых расположены центры атомов, называются узлами кристаллической решетки. Кристаллы обладают свойством симметрии, т.е. свойством совмещаться с собой при поворотах, отражениях, параллельных переносах. Наиболее важным свойством монокристаллов является их периодическая структура.

Наименьшая часть кристалла, пространственным повторением которой образуется весь кристалл, называется элементарной ячейкой. Элементарная ячейка может содержать один или несколько ионов, атомов или молекул. В целом ячейка электрически нейтральна. 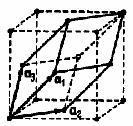Выбранную элементарную ячейку характеризуют тремя векторами основных трансляций 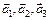совпадающими с ее тремя ребрами, сходящимися в одной точке. Объем элементарной ячейки определяется по формуле: 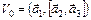. (1)

Пространственную решетку характеризуют этими же тремя векторами 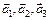, задав их длины 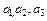, которые называются периодами кристаллической решетки и углами α₁₂, α₁₃, α₂₃ между ними; именно эти параметры содержатся во всех справочниках по структуре веществ. Если бесконечный монокристалл сместить на вектор

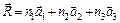n₁, n₂, n₃ – целые числа (2)

то он совместится с самим собой. Это свойство называется трансляционной симметрией. Система точек, даваемая формулой (2) называется решеткой Браве. Любое преобразование, совмещающее решетку с собой, называется преобразованием симметрии.

Различают следующие основные типы элементарных ячеек:

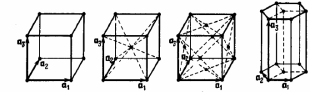
а) б) в) г)

а) простая, в которой узлы расположены в вершинах параллелепипеда;

б) объемно-центрированная – узлы расположены в вершинах и в центре параллелепипеда;

в) гранецентрированная – узлы в вершинах и центрах граней;

г) базоцентрированная – узлы в вершинах и в центрах двух противоположных граней.

В общем случае элементарная ячейка, имеющая форму параллелепипеда, не обладает симметрией кристаллической решетки. Вигнер и Зейтц показали, как можно выбрать элементарную ячейку, чтобы она обладала такой симметрией. Для этого надо выбрать некоторый атом и провести от него отрезки к ближайшим атомам. Построить через середины этих отрезков плоскости, перпендикулярные к ним. Пересечение этих плоскостей определит минимальный многогранник, содержащий внутри данный атом. Такой многогранник называется ячейкой Вигнера-Зейтца.

Узлы, направления и плоскости в кристалле обозначают с помощью индексов Миллера.

Индексы узлов. Как видно из (1), положение узла определяется заданием его координат 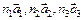. Индексы узла записывают [ n₁ n₂ n₃ ]. Для отрицательного числа знак "–" ставится над индексом, например .

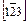Индексы направления. Для описания направления выбирается прямая, проходящая через начало координат и узел. Индекс узла одновременно является индексом направления.

Индексы плоскости ( h k l ) – набор трех целых чисел, заключенных в круглые скобки. Положение плоскости определяется заданием трех отрезков А, В, С, которые она отсекает на осях решетки:

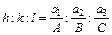(4)

На рисунке, приведенном ниже, указаны индексы Миллера для некоторых плоскостей в кристалле с простой кубической решеткой.

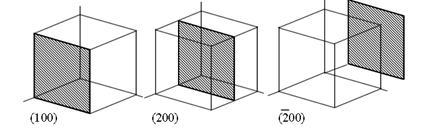
Рассмотрим множество точек 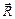, составляющих решетку Браве, и плоскую волну 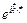. При произвольном векторе 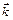такая волна не будет обладать периодичностью решетки Браве, т.е.:

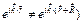. (5)

Но при определенном выборе вектора 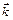будет выполняться условие

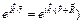. (6)

Множество волновых векторов 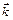называют обратной решеткой, если плоская волна 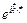имеет периодичность данной решетки Браве. Обратная решетка всегда определяется по отношению к некоторой конкретной решетке Браве.

Как следует из (6), эти векторы удовлетворяют условию

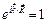. (7)

Вектор 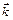можно записать в виде линейной комбинации некоторых векторов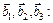

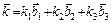. (8)

Векторы 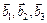называют основными векторами трансляции обратной решетки. Они связаны с основными векторами трансляции решетки Браве следующим образом:

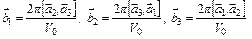, (9)

где V₀ – объем элементарной ячейки решетки Браве, определяемый по формуле (1).Векторы прямой и обратной решетки связаны соотношением:

(10)

Для кристалла с простой кубической решеткой достаточно рассматривать изменение компонент k ₁, k ₂, k ₃ вектора обратной решетки в пределах:

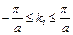, (11)

где а – длина ребра кубической элементарной ячейки.

Область значений (11) называют зоной Бриллюэна. Зона Бриллюэна в обратном пространстве строится так же, как ячейка Вигнера-Зейтца в прямом пространстве.