Квантовые статистики идеального газа. Распределение Ферми-Дирака и Бозе-Эйнштейна. Условия перехода к классической статистике, критерий вырождения.
Квантовые статистики применяются к системам, состоящим из большого числа частиц, подчиняющихся законам квантовой механики. В квантовой статистике, как и в классической, используется 6-мерное фазовое пространство (m-пространство). В таком пространстве по взаимно перпендикулярным осям откладывают декартовы координаты x, y, z и проекции импульса px, py, pz. В квантовой статистике все состояния одинаковы, если им соответствует ячейка m-пространства размером 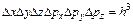 , где h – постоянная Планка. Элемент объема m-пространства, соответствующий условию, что координаты и импульс частицы изменяются в пределах[ x,x+dx ], [ y,y+dy ], [ z,z+dz ], [ px,px+dpx ], [ py, py +dpy ], [ pz,pz+dpz ] записывается в виде
, где h – постоянная Планка. Элемент объема m-пространства, соответствующий условию, что координаты и импульс частицы изменяются в пределах[ x,x+dx ], [ y,y+dy ], [ z,z+dz ], [ px,px+dpx ], [ py, py +dpy ], [ pz,pz+dpz ] записывается в виде  Состояние частицы определяется указанием ячейки m-пространства, в которую "попадает" данная частица.
Состояние частицы определяется указанием ячейки m-пространства, в которую "попадает" данная частица.
Квантовая статистика строится на принципе тождественности частиц. При этом считается, что состояние частиц не меняется при перестановке частиц внутри одной и той же ячейки фазового пространства и при перестановке между различными ячейками m-пространства.
|
|
|
Основная задача квантовой статистики состоит в нахождении равновесного (т.е. наиболее вероятного) распределения частиц по возможным квантованным значениям e1, e2,…, e k энергии e частицы.
Частицы с целым или нулевым спином (в единицах h) называются бозонами. К ним относятся:
1. К- и p-мезоны со спином 0;
2.атомы и ядра атомов с целочисленным спином;
3. фотоны.
Бозоны описываются квантовой статистикой Бозе-Эйнштейна. В данной статистике бозоны рассматриваются как идеальный газ, т.е. считается, что между частицами нет взаимодействия. Бозоны не подчиняются принципу Паули, поэтому на них не накладываются ограничения на число частиц, которые могут находиться в одной ячейке фазового m-пространства. Для бозонов характерно то, что вероятность возникновения бозона в состоянии, где уже имеется n частиц, пропорциональна n. Т.е. бозоны "любят" накапливаться в одном квантовом состоянии. Функция распределения для системы тождественных бозонов называется функцией распределения Бозе-Эйнштейна f Б. Она имеет следующий вид:
 , (1)
, (1)
где k – постоянная Больцмана, Т – термодинамическая температура, e– энергия квантового состояния, m– химический потенциал частиц. Величина m равна производной от энергии системы U по числу частиц N в ней, при условии, что объем и энтропия системы не изменяются:
 .
.
Данная функция определяет среднее число бозонов, находящихся в состоянии с энергией e при температуре Т.
|
|
|
Частицы, обладающие полуцелым спином (в единицах h) называются фермионами. К фермионам относятся:
1. электроны;
2. нуклоны (протоны и нейтроны);
3. ядра и атомы с полуцелым спином.
Фермионы описываются квантовой статистикой Ферми-Дирака. Фермионы помимо принципа тождественности подчиняются еще и принципу Паули, и в данном квантовом состоянии (или ячейке m-пространства) не может находиться более одного фермиона. Поэтому статистика Ферми-Дирака отличается от статистики Бозе-Эйнштейна.
Функция распределения для системы тождественных фермионов называется функцией распределения Ферми-Дирака f Ф. Данная функция имеет вид:
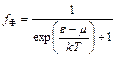 . (2)
. (2)
Она определяет среднее число фермионов в состоянии с энергией e при температуре Т.
Газы, подчиняющиеся законам классической механики, будем называть невырожденными. Для таких систем частиц применяется классическое распределение Максвелла-Больцмана. Газы починяющиеся квантовым статистикам, называют вырожденными.
Функции распределения в классической и квантовых статистиках могут быть выражены единой формулой: 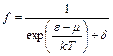 . (3)
. (3)
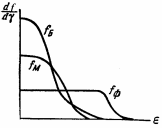 Для распределения Максвелла-Больцмана d=0, для распределения Ферми-Дирака d=+1, для распределения Бозе-Эйнштейна d= –1.
Для распределения Максвелла-Больцмана d=0, для распределения Ферми-Дирака d=+1, для распределения Бозе-Эйнштейна d= –1.
На практике расстояния между уровнями энергии поступательного движения малы по сравнению с тепловой энергией kT. Поэтому энергетический спектр частиц можно считать непрерывным. Тогда вместо среднего числа частиц на уровне энергии e вводят среднее число частиц df с энергиями между e и e+ d e:
 , (4)
, (4)
где g = 2s+1, 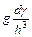 - число состояний с энергиями в интервале от e до e+ d e с учетом спина.
- число состояний с энергиями в интервале от e до e+ d e с учетом спина.
Величина df должна удовлетворять условию нормировки, выражающего постоянство числа частиц, находящихся в данном объеме:
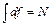 . (5)
. (5)
Определим условия, при которых квантовая статистика переходит в классическую.
Пусть энергия частицы сводится к кинетической: 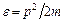 . (6)
. (6)
Как следует из (4), различие между статистиками исчезает при  . При энергиях
. При энергиях 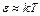 нужно, чтобы было
нужно, чтобы было 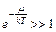 , в этом случае
, в этом случае 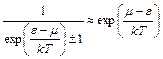 . Тогда из условия нормировки (5) находим:
. Тогда из условия нормировки (5) находим: 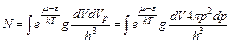 (7)
(7)
Заменим в (7) импульс на энергию с учетом (6):
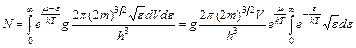 =
=
=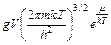 отсюда
отсюда 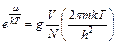 , т.е. критерием применения классической статистики является условие
, т.е. критерием применения классической статистики является условие
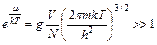 (8)
(8)
При выполнении обратного условия наступает вырождение и следует пользоваться квантовыми статистиками. В (8) входит масса частиц, температура и концентрация частиц 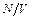 . Из (8) следует, что вырождение обусловлено следующими причинами:
. Из (8) следует, что вырождение обусловлено следующими причинами:
1. малая масса частиц;
2. большая концентрация частиц;
3. низкая температура.
16. Электроны в металлах как вырожденный Ферми-газ. Ферми-газ в астрофизических объектах: белые карлики и нейтронные звезды.
В металлах электроны ведут себя как свободные частицы идеального газа. Энергия этих электронов принимается равной
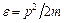 (1)
(1)
Электроны подчиняются квантовой статистике Ферми-Дирака, в которой функция распределения
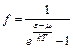 (2)
(2)
определяет среднее число частиц в квантовом состоянии с энергией e.
Вычислим среднее число электронов dN (Е), имеющих энергию в интервале [ Е, Е+dЕ ]. Учтем, что в фазовом пространстве число элементарных ячеек, определяющих число квантовых состояний электронов с импульсами от p до p+dp равно
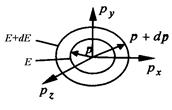
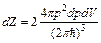 . (3)
. (3)
где множитель 2=g=2s+1=2×1/2 +1 учитывает наличие спина электронов.
Тогда число электронов dN, находящихся в состояниях dZ, равно произведению числа состояний на вероятность нахождения электронов в этих состояниях:
 . (4)
. (4)
Заменим в (4) импульс на энергию, используя (1):
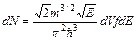 . (5)
. (5)
Тогда концентрация электронов в состояниях с энергиями [ E, E+dE ] будет равна
 , (6)
, (6)
где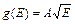 – функция плотности состояний (
– функция плотности состояний (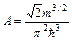 ). При Т→0 и 0< E < m функция f»1. В этом случае
). При Т→0 и 0< E < m функция f»1. В этом случае
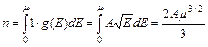 (7)
(7)
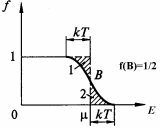 Отсюда выразим
Отсюда выразим 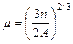 . Оценки показывают, что при концентрации электронов n ~ 1023 см–3 m»5 эВ. Этому значению энергии соответствует температура
. Оценки показывают, что при концентрации электронов n ~ 1023 см–3 m»5 эВ. Этому значению энергии соответствует температура 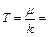

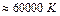 . Т.е. энергия Ферми во много раз превышает температуру, при которой существует твердое тело. Другими словами, электронный газ при комнатных температурах сильно вырожден. По этой причине электронный газ при комнатных температурах не вносит никакого вклада в теплоемкость металла. При этом все нижние состояния зоны проводимости вплоть до m заняты электронами, а все более высокие – свободны. Между ними будет находиться область шириной 2 kT, в которой состояния будут частично заполнены. В физике металлов важнейшую роль будут играть именно эти электроны, энергия которых близка к m. Эти электроны располагаются вблизи поверхности Ферми Е = m. Оценим долю этих электронов как отношение приповерхностного объема к полному:
. Т.е. энергия Ферми во много раз превышает температуру, при которой существует твердое тело. Другими словами, электронный газ при комнатных температурах сильно вырожден. По этой причине электронный газ при комнатных температурах не вносит никакого вклада в теплоемкость металла. При этом все нижние состояния зоны проводимости вплоть до m заняты электронами, а все более высокие – свободны. Между ними будет находиться область шириной 2 kT, в которой состояния будут частично заполнены. В физике металлов важнейшую роль будут играть именно эти электроны, энергия которых близка к m. Эти электроны располагаются вблизи поверхности Ферми Е = m. Оценим долю этих электронов как отношение приповерхностного объема к полному:
|
|
|
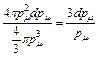 , (8)
, (8)
где dp m – область размытия поверхности Ферми. Используем для оценки (1), полагая E = m и d m=2 kT, тогда
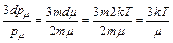 (9)
(9)
При комнатных температурах Т ~ 300 К эта величина принимает значение ~0,01~1%. То есть при комнатных температурах доля таких электронов мала и основной вклад в теплоемкость вносит кристаллическая решетка, а электроны практически не влияют на теплоемкость. Но при понижении температуры до Т→0, теплоемкость решетки резко падает и данные электроны начинают влиять на теплоемкость. При этом вклад электронной теплоемкости пропорционален температуре. Покажем это. Теплоемкость, приходящаяся на один электрон равна 3k/2. Доля таких электронов 3kT/m, их концентрация – n, тогда электронная теплоемкость
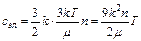 , т.е сэл ~ Т.
, т.е сэл ~ Т.
Электронный газ в вырожденном состоянии находится в белых карликах. Белые карлики образуются из красных гигантов, когда их плотные ядра в результате термоядерных реакций сбрасывают оболочку и начинают сжиматься. Массы белых карликов порядка солнечной, а размеры порядка Земли. Они характеризуются очень большими плотностями (109–1010 кг/м3) и высокими температурами. Кроме того, высокая концентрация электронов в вырожденном состоянии создает очень высокое давление внутри звезды. Белый карлик существует за счет равновесия между давлением электронного газа и гравитационным давлением. Из-за вырождения электронного газа вещество недр белых карликов отличается высокой прозрачностью и теплопроводностью. Вследствие этого в недрах белого карлика не могут возникать большие перепады температур. Перепад температур происходит в тонком приповерхностном слое, где электронный газ не вырожден. Толщина этого слоя около 1% радиуса карлика. На границе поверхности этого слоя температура около нескольких тысяч кельвинов, при движении к центру возрастает до десятков миллионов и затем вплоть до центра почти не меняется.
|
|
|
При высоких плотностях звезды начинается процесс поглощения ядрами электронов с образованием нейтронов (происходит К-захват). Вследствие этого уменьшается количество электронов и соответственно давление электронного газа, поддерживающего звезду в равновесии. Это приводит к дальнейшему гравитационному сжатию звезды и более интенсивному К-захвату. В конце концов звезда преимущественно будет состоять из нейтронов. Плотность такой звезды порядка ядерной плотности, радиус звезды порядка 10 км. Такие звезды называются нейтронными. Существование таких звезд было предсказано еще в 1938 году Р. Оппенгеймером. Нейтронные звезды были открыты в 1967 году, когда с помощью радиотелескопа обнаружили источник, посылающий строго периодические радиоимпульсы. Такие источники были названы пульсарами. Периоды излучения радиоволн пульсаров от 0,001 до 3 с. Мощность излучения может в десятки тысяч раз превышать мощность излучения Солнца. Пульсары были отождествлены с нейтронными звездами. Магнитные поля нейтронных звезд обладают очень высокими напряженностями и направление магнитного поля, как правило, не совпадает с осью вращения звезды, вследствие этого магнитный момент пульсара вращается и, следовательно, изменяется во времени. Изменяющийся магнитный момент излучает электромагнитные волны, при этом излучение сосредоточено в пределах узкого конуса. Когда Земля попадает в пределы этого конуса, обнаруживается всплеск радиоизлучения. Размеры звезды очень маленькие, поэтому конус звезды вращается очень быстро, этим и объясняются малые периоды излучения пульсаров.
Рассмотрим применение статистики Бозе-Эйнштейна к частицам с целым спином. Системы таких частиц будем рассматривать как газ бозонов.
Среднее число частиц, имеющих энергии в интервале [e, e+de]:
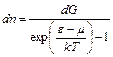 , (1)
, (1)
где m – химический потенциал, dG – число квантовых состояний с энергиями в интервале [e, e+de]:
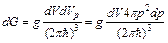 , (2)
, (2)
 , s спин частицы. Заменим в (2) импульс на энергию, полагая, что частицы являются идеальным газом, т.е. обладают только кинетической энергией
, s спин частицы. Заменим в (2) импульс на энергию, полагая, что частицы являются идеальным газом, т.е. обладают только кинетической энергией 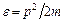 , тогда
, тогда 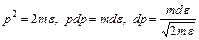 и
и
 ,
,
где 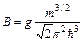 . (3)
. (3)
Для dn записывают условие нормировки, соответствующее условию, что число частиц N в системе постоянно:
 . (4)
. (4)
Химический потенциал m в (1) может быть только меньше нуля, в случае m> 0 функция распределения становится отрицательной, чего не может быть, т.к. эта функция определяет среднее число частиц.
При этом m возрастает с уменьшением температуры и может принять максимальное значение m=0 при определенной температуре Т0.
Это значение температуры находят из условия нормировки (4):
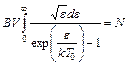 . (5)
. (5)
Введем новую переменную 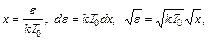 ,
,
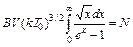 ,
, 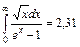 (6)
(6)
Отсюда  . (7)
. (7)
Т0 называется температурой вырождения. При температуре ниже Т0 происходит переход большинства частиц в состояния с наименьшей энергией. Этот процесс называется бозе-конденсацией. При этом отметим, что никакой конденсации в обычном смысле этого слова не происходит. Распределение частиц в пространстве остается равномерным. Речь идет о конденсации в пространстве импульсов. Большинство частиц переходят в состояния с нулевым значением импульса.
Для всех известных бозе-газов температураТ0 мала и вещества переходят в твердое состояние раньше, чем может наступить бозе-конденсация.
Для 4Не Т0 равна 2,8 К. Гелий является единственным веществом, которое остается в жидком состоянии при температурах близких к абсолютному нулю. При температуре 2,8 К он претерпевает фазовое превращение второго рода (т.е. превращение без поглощения или выделения теплоты и без изменения плотности). Жидкая фаза при температурах выше 2,8 К называется гелий I, а жидкая фаза при температурах ниже 2,8 К – гелий II.
В 1938 г. П.Л. Капица открыл явление сверхтекучести для гелия II. Это явление проявляется в том, что гелий II, протекая по узким каналам или щелям, не обнаруживает никакой вязкости. Другая особенность гелия II проявляется в том, что на поверхности тел, погруженных в гелий, появляется тонкая пленка. Толщина этой пленки около 100 атомных слоев. Благодаря этому пустая пробирка, опущенная в ванну с гелием II, начинает наполняться жидкостью, даже если ее верхний конец расположен выше уровня жидкости (рис. а). Наполнение пробирки жидкостью продолжается до тех пор, пока уровни жидкости в пробирке и ванне не сравняются. Если пробирку приподнять, то она опустошается (рис.б). Опустошение продолжается и в том случае, когда, когда пробирка приподнята над уровнем жидкости в ванне целиком. В этом случае образуются капли с наружной поверхности дна пробирки (рис. в).
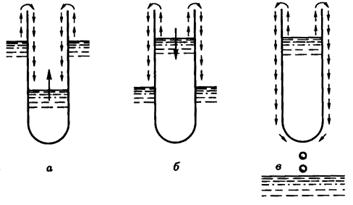
В этих опытах пленка гелия II работает как сифон, при этом движущую силу для жидкости дает разность гравитационных потенциалов между концами пленки.
 2014-02-02
2014-02-02 3928
3928








