В предыдущем параграфе мы видели, что при чистом изгибе возникают только нормальные напряжения. Соответственно внутренние силы приводятся к изгибающему моменту в сечении.
При поперечном изгибе в сечении бруса возникает не только изгибающий момент, но и перерезывающая сила. Эта сила является равнодействующей элементарных сил, лежащих в плоскости сечения (рис.5.8).
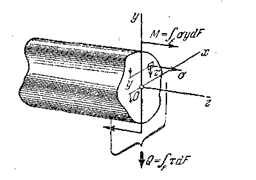
Рис. 5.8
Таким образом, при поперечном изгибе возникают не только нормальные, но и касательные напряжения. Возникновение касательных напряжений 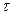 сопровождается появлением угловых деформаций
сопровождается появлением угловых деформаций 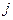 . Поэтому нарушается гипотеза плоских сечений. На рис 5.9 показана типичная картина искривления поперечных сечений.
. Поэтому нарушается гипотеза плоских сечений. На рис 5.9 показана типичная картина искривления поперечных сечений.
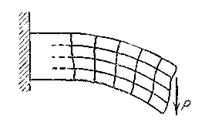
Рис. 5.9
Теоретически и экспериментально доказано, что искажение плоскости поперечных сечений заметным образом не сказывается на величине нормальных напряжений. Таким образом, нормальные напряжения при поперечном изгибе вычисляются по тем же формулам, что и при чистом изгибе
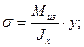
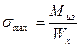 .
.
Тем самым гипотеза плоских сечений распространяется на поперечный изгиб.
Теперь определим приближенно величину касательных напряжений 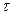 при поперечном изгибе. Выделим из бруса элемент длиной
при поперечном изгибе. Выделим из бруса элемент длиной 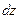 (рис. 5.10).
(рис. 5.10).
При поперечном изгибе моменты, возникающие в левом и правом сечениях элемента, не одинаковы и отличаются на величину 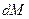 .
.
Продольным горизонтальным сечением, проведенным на расстоянии 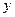 от нейтрального слоя (рис. 5.10,б) разделим этот элемент на две части и рассмотрим условие равновесия верхней части. С правой стороны напряжения в каждой точке больше, чем с левой, т.к. изгибающий момент справа больше чем слева (рис.5.10,б).
от нейтрального слоя (рис. 5.10,б) разделим этот элемент на две части и рассмотрим условие равновесия верхней части. С правой стороны напряжения в каждой точке больше, чем с левой, т.к. изгибающий момент справа больше чем слева (рис.5.10,б).
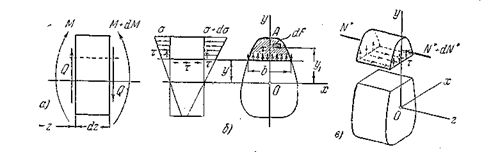
Рис. 5.10
Равнодействующая нормальных сил 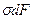 в левом сечении в пределах заштрихованной площади
в левом сечении в пределах заштрихованной площади 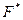 равна
равна
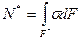
или согласно формуле (5.8)
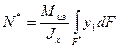 ,
,
где 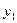 — текущая ордината площадки
— текущая ордината площадки 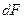 (рис. 5.10,б),
(рис. 5.10,б),
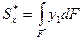 — статический момент относительно оси
— статический момент относительно оси 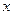 части площади, расположенной выше продольного сечения
части площади, расположенной выше продольного сечения 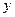 .
.
Тогда
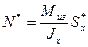 .
.
В правом сечении нормальная сила будет другой
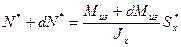 .
.
Разность этих сил в правом и левом сечениях равна
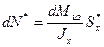 .
.
Эта разность должна уравновешиваться касательными силами, возникающими в продольном сечении элемента (рис. 5.10,б и в).
В качестве приближения примем, что касательные напряжения распределены по ширине сечения 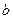 равномерно.
равномерно.
Тогда 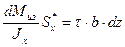 .
.
Откуда 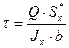 (5.11)
(5.11)
Эта формула позволяет вычислять напряжения в продольных сечениях бруса. Напряжения в поперечных сечениях равны им по закону парности.
Таким образом, формула позволяет вычислять касательные напряжения в любых точках 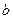 по высоте поперечного сечения.
по высоте поперечного сечения.
Рассмотрим распределение касательных напряжений для некоторых типов поперечных сечений.
Прямоугольное сечение (рис. 5.11).
Возьмем произвольную точку 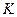 , отстоящую от нейтральной оси
, отстоящую от нейтральной оси 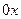 на расстоянии
на расстоянии 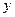 . Проведем через эту точку сечение параллельно оси
. Проведем через эту точку сечение параллельно оси 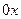 ; ширина этого сечения —
; ширина этого сечения — 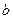 .
.
Статический момент отсеченной (заштрихованной) части равен
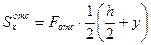 ;
; 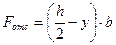 ,
,

Рис. 5.11
Следовательно,
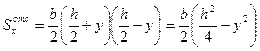 .
.
Как известно,
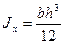 .
.
Подставляя полученные значения в формулу (5.11), имеем
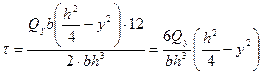 (5.12)
(5.12)
Формула (5.12) показывает, что касательные напряжения по высоте сечения изменяются по закону квадратной параболы. При  получим
получим 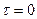 , а при
, а при 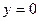 имеем
имеем 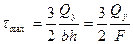 .
.
Двутавровое сечение (рис. 5.12). Характерной особенностью этого сечения является резкое изменение ширины сечения при переходе от стенки двутавра к его полке. В основном поперечную силу воспринимает стенка, а на долю полок приходится небольшая величина.
Рассмотрим произвольную точку 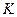 (рис. 5.12). Проведем через эту точку линию параллельную оси
(рис. 5.12). Проведем через эту точку линию параллельную оси 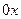 . Статический момент площади верхней отсеченной части (заштрихована на рис. 5.12) может быть найден как сумма статических моментов площадей
. Статический момент площади верхней отсеченной части (заштрихована на рис. 5.12) может быть найден как сумма статических моментов площадей 
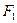 и
и 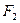 :
:
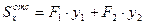 .
.
Эта формула справедлива, когда точка 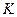 находится в пределах вертикальной стенки, т.е. пока величина
находится в пределах вертикальной стенки, т.е. пока величина 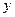 лежит в пределах
лежит в пределах 
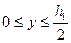 . Эпюра касательных напряжений для вертикальной стенки имеет вид, показанный на рис. 5.12.
. Эпюра касательных напряжений для вертикальной стенки имеет вид, показанный на рис. 5.12.
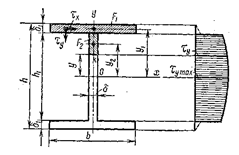
Рис. 5.12
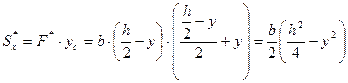 .
.
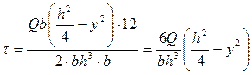 .
.
 2014-02-02
2014-02-02 551
551








