Понятие статистической гипотезы

СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ

Статистическая гипотеза (H, лат. hypothesis) – предположение о свойстве генеральной совокупности, которое можно прове­рить, опираясь на данные выборки.

Например, гипо­теза о том, что средняя в генеральной совокупности равна не­которой величине H: 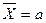, или о том, что генеральная сред­няя больше некоторой величины: H: .

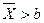Различают простые и сложные гипотезы.

− Простая – однозначно характеризует параметр распределения случайной величины. Например, H: .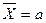

− Сложная – состоит из конечного или бесконечного числа простых гипотез, при этом указывается некоторая об­ласть вероятных значений параметра. Например, H: 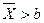. Она состоит из множества простых гипотез: H: 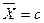, где с — любое число, большее b.

Гипотезы о параметрах генеральной совокупности (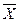, 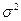) назы­ваются параметрическими, о распределениях – непараметри­ческими.

Нулевая гипотеза (H₀) – гипотеза о том, что две или более сравниваемые величины не отличаются. При этом предполагается, что выявленное по дан­ным отличие носит случайный характер.

H₀ отвергается, когда по выборке по­лучается результат, который при истинности выдвинутой H₀ маловероятен. Границей невозможного или маловероятного обычно считают γ = 0,05, т.е. 5%, или 0,01, 0,001 – уровень значимости.

Проверка H₀ осуществляется с помощью статистического критерия – определенное пра­вило, устанавливающее условия, при которых проверяемую нулевую гипотезу следует либо отклонить, либо не отклонить.

Основными статистическими критериями являются

− t-критерий Стьюдента,

− F-критерий Фишера,

− χ² (хи-квадрат) критерий Пирсона.

Принятие или отклонение H₀ определяется границами критической области и области допустимых значений.

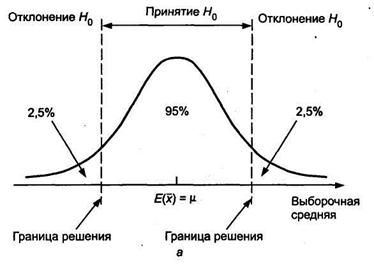
Рис. 10.1. Границы критической области и область допустимых значений при

5%-м уровне значимости

Критическая область – область, попадание значения статистического критерия в которую приводит к от­клонению H₀. Вероятность попадания значения критерия в эту область равна принятому уровню значимости γ.

Область допустимых значений дополняет критическую об­ласть. Если значение критерия попадает в область допустимых значений, это свидетельствует о том, что выдвинутая гипотеза H₀ не противоречит фактическим данным (H₀ не отклоняется).

Точки, разделяющие критическую область и область до­пустимых значений, называются критическими точками или границами критической области.

Если вычисляемое значение критерия попадает в крити­ческую область, нулевая гипотеза отклоняется, т.к. она противоречит фактическим данным.