Используется, если значения признака являются результатом какого-либо редко возникающего события среди наблюдаемых единиц, и с увеличением значений признака вероятность наступления события падает. Например, распределение автомобилей по числу неисправностей; распределение числа заявок, поступающих на телефонную станцию или ремонтную мастерскую.
Выражается формулой
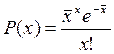 ,
,
где P (x) – вероятность того, что признак имеет то или иное значение (рис. 10.2).
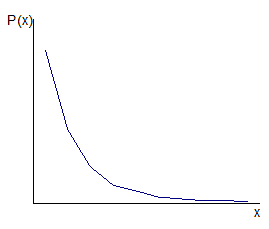
Рис. 10.2. Кривая распределения Пуассона
Расчет теоретических частот кривой распределения Пуассона.
1. По выборочным данным рассчитывается 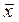 .
.
2. По таблицам определяется 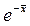 .
.
3. Рассчитываются теоретические частоты 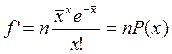 .
.
 2014-02-02
2014-02-02 498
498








