2014-02-02
439
Параметры α и β рассчитываются методом наименьших квадратов (МНК) по данным об n значениях признаков x и y. Исходное условие МНК для парной регрессии имеет вид:
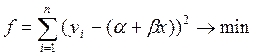
То есть МНК позволяет получить такие оценки параметров a и b, при которых сумма квадратов отклонений фактических значений зависимой переменной y от расчетных (теоретических) минимальна.
Чтобы найти минимум этой функции необходимо вычислить производные по каждому из параметров α и β и приравнять их к нулю:
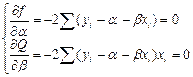Þ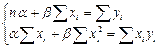
Если первое уравнение разделить на n, то получится:
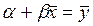Þ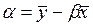 
Решая систему уравнений далее, находится коэффициент регрессии β:
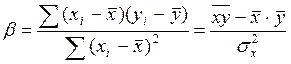
где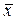 
- среднее значение x, 
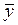- среднее значение y, 
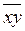- среднее значение произведения xy, 
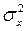- дисперсия показателя x.
Пример 11.2. По данным примера 11.1. определить параметры и построить график уравнения парной линейной регрессии, определить тесноту связи с помощью парного коэффициента корреляции.
, 
,
,
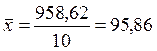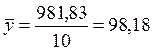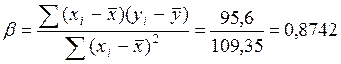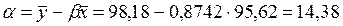
Тогда уравнение регрессии будет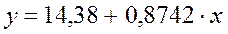 
.
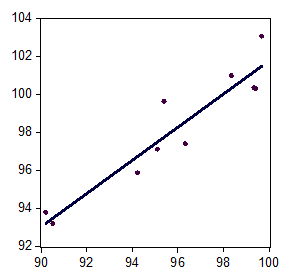
Рис. 11.2. Уравнение парной регрессии и фактические данные
|
|
|
