Линия, описываемая движущейся материальной точкой относительно выбранной системы отсчета, называется траекторией ее движения. В зависимости от формы траектории различают прямолинейное и криволинейное движения.
 Рис.1.2 Рис.1.2 | Рассмотрим движение материальной точки вдоль траектории 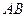 (рис.1.2). Длина криволинейного участка (рис.1.2). Длина криволинейного участка 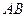 называется длиной пути называется длиной пути 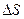 . Это скалярная величина, являющаяся функцией времени . Это скалярная величина, являющаяся функцией времени 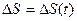 . Вектор . Вектор 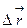 , проведенный из начального положения , проведенный из начального положения 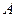 точки в положение ее точки в положение ее 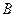 в данный момент времени, называется в данный момент времени, называется |
вектором перемещения. Это приращение радиус-вектора точки за время 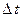 . При прямолинейном движении в одном направлении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения равен пройденному пути
. При прямолинейном движении в одном направлении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения равен пройденному пути 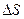 :
:
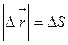 .(1.1.3)
.(1.1.3)
Единица перемещения - 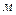 .
.
1.3. Скорость
Скорость – это векторная величина, определяющая быстроту и направление движения точки в данный момент времени.
Вектор средней скорости точки  за время
за время 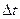 определяется отношением приращения радиус-вектора точки
определяется отношением приращения радиус-вектора точки 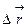 к промежутку времени
к промежутку времени 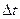 :
:
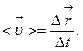 (1. 1.4)
(1. 1.4)
Единица скорости - 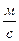 .
.
Мгновенная скорость 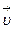 (скорость) – векторная величина, равная первой производной по времени от радиус-вектора
(скорость) – векторная величина, равная первой производной по времени от радиус-вектора 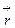 движущейся точки:
движущейся точки:
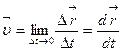 . (1. 1.5)
. (1. 1.5)
Вектор 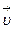 направлен по касательной к траектории точки в сторону ее движения. Модуль скорости определяется выражением:
направлен по касательной к траектории точки в сторону ее движения. Модуль скорости определяется выражением:
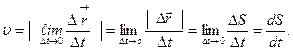 (1.1.6)
(1.1.6)
Откуда 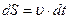 , (1.1.7)
, (1.1.7)
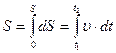 . (1.1.8)
. (1.1.8)
При равномерном движении (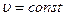 ) формула пути имеет вид:
) формула пути имеет вид:
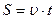 . (1.1.9)
. (1.1.9)
 2014-02-02
2014-02-02 3378
3378
