Ускорение - это векторная величина, характеризующая быстроту изменения скорости материальной точки по модулю и направлению.
Вектор среднего ускорения точки 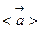 за время
за время 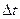 определяется отношением изменения скорости
определяется отношением изменения скорости 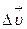 к промежутку времени
к промежутку времени 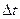 :
:
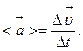 (1.1.10)
(1.1.10)
Единица ускорения - 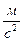 .
.
Мгновенное ускорение (ускорение) – векторная величина, равная первой производной по времени от скорости точки или второй производной по времени от ее радиус-вектора:
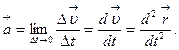 (1.1.11)
(1.1.11)
С учетом (1.1.6) модуль ускорения равен 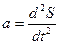 (1.1.12)
(1.1.12)
Движение с постоянным ускорением (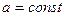 ) называется равнопеременным (равноускоренным, если
) называется равнопеременным (равноускоренным, если  , и равнозамедленным, если
, и равнозамедленным, если 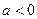 ).
).
Обозначим скорость в начальный момент времени (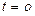 ) через
) через 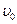 . Тогда из зависимости (1.1.11)
. Тогда из зависимости (1.1.11) 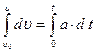 можно определить закон скорости при равнопеременном движении:
можно определить закон скорости при равнопеременном движении: 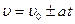 (1.1.13)
(1.1.13)
Подставив (1.1.13) в (1.1.8), получим:
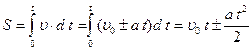 . (1.1.14)
. (1.1.14)
Направление вектора 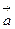 совпадает с направлением вектора
совпадает с направлением вектора 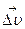 . Поэтому при прямолинейном ускоренном движении направление вектора
. Поэтому при прямолинейном ускоренном движении направление вектора 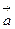 совпадает с направлением вектора
совпадает с направлением вектора 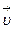 , а при замедленном движении противоположно ему.
, а при замедленном движении противоположно ему.
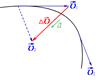 Рис.1.3 Рис.1.3 | При криволинейном движении (рис.1.3) вектор 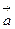 , так же как и вектор , так же как и вектор 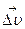 , направлен в сторону вогнутости траектории. Удобно разложить вектор , направлен в сторону вогнутости траектории. Удобно разложить вектор 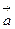 на две компоненты (рис.1.4): на две компоненты (рис.1.4): | 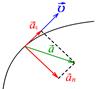 Рис.1.4 Рис.1.4 |
тангенциальную (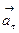 ) в направлении вектора
) в направлении вектора 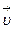 и нормальную (
и нормальную (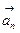 ), перпендикулярно ему, так, чтобы
), перпендикулярно ему, так, чтобы 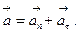 (1.1.15)
(1.1.15)
Тангенциальное ускорение характеризует быстроту изменения величины скорости 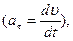 нормальное – быстроту изменения направления вектора скорости.
нормальное – быстроту изменения направления вектора скорости.
Можно показать, что модуль нормального ускорения при равномерном вращении точки по окружности радиуса 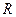 определяется формулой
определяется формулой
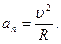 (1.1.16)
(1.1.16)
Модуль полного ускорения точки равен: 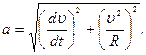 (1.1.17)
(1.1.17)
Значения составляющих ускорения при различных видах поступательного движения точки приведены в табл.1.1.
Таблица 1.1
Движение | Тангенциальное ускорение 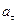 | Нормальное ускорение 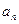 |
| Равномерное прямолинейное | 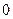 | 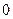 |
| Равнопеременное прямолинейное | 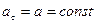 | 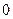 |
| Равномерное вращение | 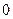 | 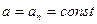 |
| Равнопеременное криволинейное | 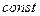 | 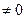 |
 2014-02-02
2014-02-02 7246
7246
