Уравнение Максвелла, векторный потенциал, граничные условия

Аксиоматика макроскопической электродинамики

Основные определения и понятия. Характеристики антенн

Антенна-устройство, преобразующее подводимую от источника по фидерному электромагнитную энергию, в энергию электромагнитного поля.

Диаграмма направленности - угловая зависимость амплитуды вектора напряженности электрического поля, создаваемого антенной.

Ширина главного лепестка - интервал углов, в пределах которого уровень главного лепестка уменьшается по отношении к максимальному значению не более чем на заданную величину (обычно эта величина равна -3 дБ).

Уровень боковых лепестков – уровень поля максимального бокового лепестка (обычно это лепесток, примыкающий к главному) по отношению к максимальному значению поля в главном лепестке.

Входное сопротивление – сопротивление антенны на входных зажимах.

Полоса рабочих частот - интервал частот, в пределах которого характеристики антенны по заданному критерию остаются постоянными.

Электродинамика – аксиоматическая наука, основанная на утверждениях, не требующих доказательств (уравнениях Максвелла), которые в дифференциальном виде имеют вид:

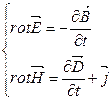(2.1)

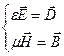(2.2)

Уравнения сформулированы относительно векторов 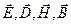- вектора напряженности электрического поля, вектора электрической индукции, вектора напряженности магнитного поля, вектора магнитной индукции, каждый из которых является функцией 4-х переменных - трех координат и времени 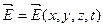. Дифференциальные уравнения Максвелла описывают поле в любой точке пространства кроме границы раздела сред, где производных не существует, поэтому они должны быть дополнены т.н. граничными условиями, т.е. условиями, накладываемыми на компоненты векторов в обеих средах в непосредственной близости к границе раздела.

Если электромагнитные сигналы представляют собой гармонические колебания 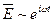, то уравнения Максвелла можно записать на основе метода комплексных амплитуд:

(2.3)

В уравнения (2.1-2.3) 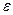и - диэлектрическая и магнитная проницаемости среды. В общем случае диэлектрическая и магнитная проницаемости среды являются тензором, но мы будем рассматривать самый простой случай, когда 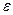и являются просто константами. Таким образом, уравнение (2.1) с учетом гармонической зависимости полей от времени принимает следующий вид:

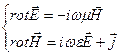
Оператор rot (ротор) может быть записан в виде определителя:

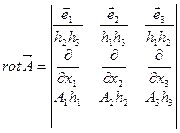
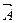- вектор, над которым берется операция ротора. 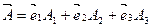, где 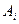- проекции вектора 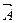на оси координат.

- метрические коэффициенты (коэффициенты Ламе) данной криволинейной системы координат.

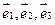- единичные вектора (орты) данной криволинейной системы координат

Пример: декартовая система координат.

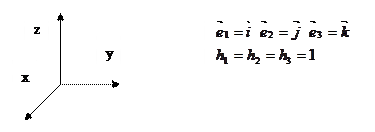
Рис.2.1.Декартовая система координат

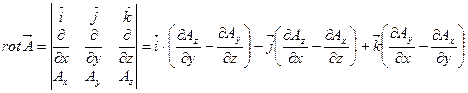
Для упрощения решения уравнений Максвелла вводится понятие векторного потенциала электрического (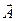) и магнитного () типа. Векторные потенциалы определяются следующим способом:

(2.4)

Из определений (4) и уравнений Максвелла следует:

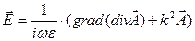(2.5)

где div – это пространственная производная от вектора, являющаяся скаляром:

,

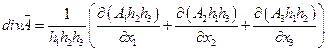в декартовой системе координат: .

grad – пространственная производная от скаляра, являющаяся вектором. В обобщенной криволинейной системе координат градиент некоторой скалярной функции 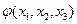выглядит таким образом:

.

В случае, если поле порождается током проводимости, протекающим в некотором объеме , векторный потенциал может быть вычислен в результате интегрирования следующим способом:

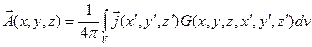
Последнее соотношение называют теоремой запаздывающих потенциалов.

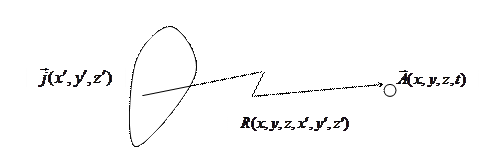
Рис. 2.1 К теореме запаздывающих потенциалов

Где G – функция Грина: ,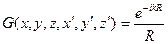

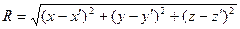.- расстояние межу точкой наблюдения и точкой интегрирования.

Тут используются две координатные системы, вложенные друг в друга. То есть 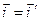, , 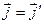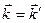. Точка (x,y,z) – это точка наблюдения. Координаты 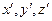- это координаты всех точек, где имеет место ток, то есть координаты точек области интегрирования, которые не выходят за рамки объема .

Сферическая система координат:

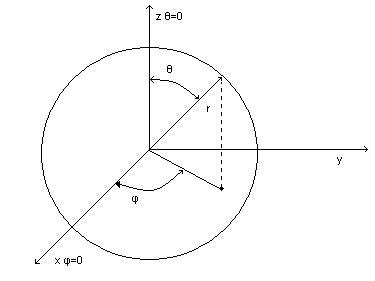
Рис. 2.3.

Для сферической системы координат, представленной на рис. 2.3 метрические коэффициенты принимают вид: , , .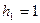

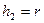Для цилиндрической системы координат метрические коэффициенты принимают вид: , , .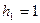

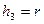Скалярное и векторное произведение векторов:

Вектор А всегда представим в n-мерном пространстве в ви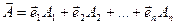де: , где 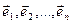- базисные вектора данного пространства. Например для декартового трехмерного пространства 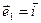, , 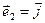, 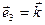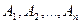представляют собой проекции вектора А на оси координат.

Скалярное произведение обозначается как или 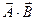и находится по формуле: , где 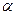- угол между вектором A и B.

Результатом векторного произведения является вектор, перпендикулярный сомножителям: 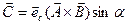. Таким образом, вектор 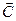имеет направление перпендикулярное векторам 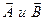и удовлетворяющее правилу буравчика.