2014-02-02
421
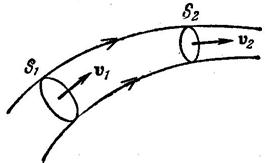
Рассмотрим движение идеальной жидкости - сплошной среды, сжимаемостью и вязкостью которой можно пренебречь. Выделим в ней некоторый объем, в нескольких точках которого определены векторы скорости движения частиц жидкости в момент времени 
. Если картина векторного поля со временем остается неизменной, то такое движение жидкости называется установившимся. При этом траектории частиц представляют собой непрерывные и не пересекающиеся линии. Их называют линиями тока, а объем жидкости, ограниченный линиями тока, трубкой тока (рис.5.1).
Поскольку частицы жидкости не пересекают поверхность такой трубки, ее можно рассматривать как реальную трубку с неподвижными для жидкости стенками. Выделим в трубке тока произвольные сечения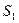 
и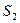 
перпендикулярные направлению скорости частиц в сечениях 
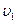и 
, соответственно (рис.5.1).
За малый промежуток времени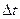 
через эти сечения протекают объемы жидкости
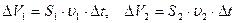. (1.6.1)
Так жидкость несжимаема 
и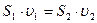 
. И тогда для любого сечения трубки тока имеет место равенство
