Рис.5.1
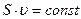 . (1.6.2)
. (1.6.2)
Оно называется уравнением неразрывности струи. В соответствии с (1.6.2) там, где сечение меньше, скорость течения жидкости больше и наоборот.
Пусть рассматриваемые сечения трубки тока идеальной жидкости малы, так что можно считать величины скорости 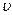 и давления
и давления 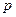 в них постоянными, т.е.
в них постоянными, т.е. 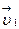 и
и 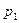 , в сечении
, в сечении 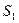 и
и 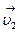 ,
, 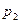 в
в 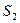 .
.
При движении жидкости за малый промежуток времени 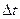 сечение
сечение 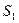 , переместится в положение
, переместится в положение  пройдя путь
пройдя путь 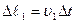 , а сечение
, а сечение 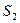 - в положение
- в положение 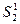 , пройдя
, пройдя 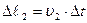 . Объем жидкости, заключенный между сечениями
. Объем жидкости, заключенный между сечениями 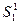 и
и 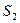 вследствие уравнения неразрывности будет
вследствие уравнения неразрывности будет 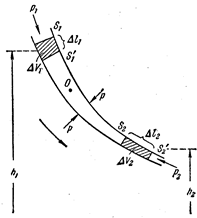 равен объем жидкости, заключенному в промежутке между
равен объем жидкости, заключенному в промежутке между 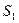 и
и 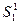 . Трубка имеет некоторый наклон и центры ее сечений
. Трубка имеет некоторый наклон и центры ее сечений 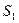 и
и 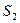 находятся на высотах
находятся на высотах 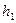 и
и 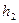 над заданным
над заданным
Рис. 5.2 горизонтальным уровнем (рис.5.2).
Учитывая что 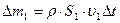 и
и 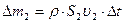 , изменение полной энергии выделенной массы жидкости, расположенной в начальный момент между сечениями
, изменение полной энергии выделенной массы жидкости, расположенной в начальный момент между сечениями 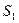 и
и  , может быть представлено в виде
, может быть представлено в виде
 . (1.6.3)
. (1.6.3)
Это изменение, согласно закону сохранения энергии, обусловлено работой внешних сил. В данном случае это силы давления 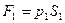 и
и 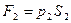
 , действующие, соответственно, на сечения
, действующие, соответственно, на сечения 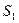 и
и 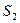 , где
, где 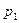 и
и 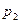 соответствующие давления. Для любого сечения трубки тока
соответствующие давления. Для любого сечения трубки тока
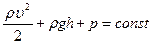 , (1.6.4)
, (1.6.4)
где 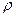 - плотность жидкости Равенство (1.6.4) выражает основной закон гидродинамики, которое называется также уравнением Бернулли по имени ученого, получившего его впервые.
- плотность жидкости Равенство (1.6.4) выражает основной закон гидродинамики, которое называется также уравнением Бернулли по имени ученого, получившего его впервые.
 2014-02-02
2014-02-02 505
505








