2014-02-02
511
Течение жидкости, при котором каждый ее слой скользит относительно других таких же слоев, и отсутствует их перемешивание, называется ламинарным или слоистым. Если внутри жидкости происходит образование вихрей и интенсивное перемешивание слоев, то такое течение называется турбулентным.
Установившееся (стационарное) течение идеальной жидкости является ламинарным при любых скоростях. В реальных жидкостях между слоями возникают силы внутреннего трения, т.е. реальные жидкости обладают вязкостью. Поэтому, каждый из слоев тормозит движение соседнего слоя. Величина силы внутреннего трения пропорциональна площади соприкосновения слоев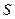 
и градиенту скорости 
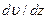, т.е.
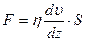, (1.7.1)
где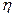 
- коэффициент пропорциональности, называемый коэффициентом вязкости. Единицей его является 
(Паскаль- секунда). Вязкость зависит от рода жидкости и от температуры. С ростом температуры вязкость уменьшается.
Если сила внутреннего трения 
невелика и скорость течения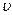 
мала, то движение практически является ламинарным. При больших силах внутреннего трения нарушается слоистый характер течения, начинается интенсивное перемешивание, т.е. происходит переход к турбулентности. Условия этого перехода при течении жидкости по трубам определяется величиной 
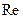кр, называемой числом Рейнольдса
|
|
|
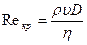, (1.7.2)
где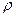 
- плотность жидкости, 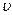- средняя по сечению трубы скорость течения, 
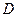- диаметр трубы. Опыты показывают, что при 
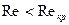течение ламинарное, при 
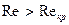оно становится турбулентным. Для труб круглого сечения радиуса 
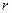число Рейнольдса 
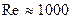. Влияние вязкости приводит к тому, что при 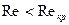скорость течения по трубе круглого сечения у различных слоев оказывается разной. Ее среднее значение определяется формулой Пуазейля
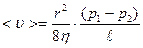, (1.7.3)
где 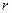- радиус трубы, (
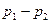)- разность давлений на концах трубы, 
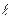- ее длина.
Влияние вязкости обнаруживается и при взаимодействии потока с неподвижным телом. Обычно, в соответствии с механическим принципом относительности, рассматривается обратная задача, Например, Стоксом установлено, что при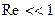 
на шар, движущийся в жидкости, действует сила трения
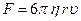, (1.7.8)
где r- радиус шарика, 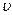- скорость его движения. Формула Стокса (1.7.8) в лабораторном практикуме применяется для определения коэффициента вязкости 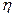жидкостей.
