Чтобы в реальной колебательной системе получить незатухающие колебания, необходимо компенсировать потери энергии при помощи какого-либо периодически действующего фактора, изменяющегося по гармоническому закону  . При механических колебаниях таким фактором является вынуждающая сила
. При механических колебаниях таким фактором является вынуждающая сила 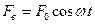 .
.
Дифференциальное уравнение вынужденных колебаний системы имеет вид:
 или
или 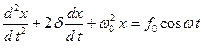 , (1.8.20)
, (1.8.20)
где 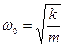 – циклическая частота свободных незатухающих колебаний;
– циклическая частота свободных незатухающих колебаний;
Это линейное неоднородное дифференциальное уравнение. Его решение равно сумме общего решения 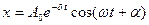 однородного уравнения и частного решения неоднородного уравнения. Можно показать, что частное решение имеет вид
однородного уравнения и частного решения неоднородного уравнения. Можно показать, что частное решение имеет вид 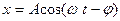 , где
, где 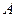 и
и 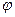 задаются формулами
задаются формулами
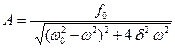 и
и 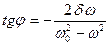 . (1.8.21)
. (1.8.21)
Амплитуда 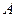 вынужденных колебаний максимальна при частоте
вынужденных колебаний максимальна при частоте 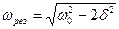 , которая
, которая
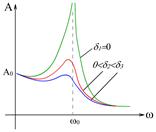 Рис.5.7 Рис.5.7 |
называется резонансной частотой 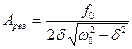 . Если
. Если 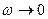 , то все кривые приходят к одному и тому же, отличному от нуля, предельному значению
, то все кривые приходят к одному и тому же, отличному от нуля, предельному значению 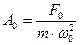 , называемому статическим отклонением. Если
, называемому статическим отклонением. Если 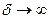 , то все кривые асимптотически стремятся к нулю. Если
, то все кривые асимптотически стремятся к нулю. Если 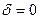 , т. е. затухания колебаний нет, то
, т. е. затухания колебаний нет, то  , и амплитуда при этом становится бесконечно большой. Поскольку в реальных системах
, и амплитуда при этом становится бесконечно большой. Поскольку в реальных системах 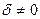 , амплитуда достигает своего максимального значения и остается конечной. Приведенная на рис. 5.7 совокупность кривых называется резонансными кривыми.
, амплитуда достигает своего максимального значения и остается конечной. Приведенная на рис. 5.7 совокупность кривых называется резонансными кривыми.
Лекция 3.
IX. Волны.
Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). Механическими (упругими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими.
 2014-02-02
2014-02-02 1219
1219

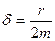 –
– 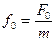 .
.






