2014-02-02
684
Затуханием колебаний называется постепенное их ослабление с течением времени, обусловленное потерей энергии колебательной системой. Механические колебания затухают главным образом из-за трения.
В вязкой среде на колеблющуюся механическую систему кроме квазиупругой силы 
действует еще сила сопротивления, которая при малых скоростях пропорциональна скорости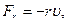 
(
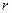– коэффициент сопротивления).
Дифференциальное уравнение свободных затухающих колебаний имеет вид:
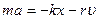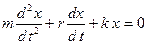или 
или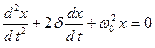 
, (1.8.16)
где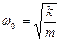 
– циклическая частота свободных незатухающих колебаний той же системы (при 
), 
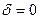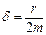– коэффициент затухания.
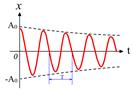Рис.5.6
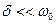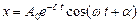| В случае малых затуханий ( ) решением этого уравнения является функция  , график которой приведен на рис.5.6 сплошной линией. Амплитуда колебаний  (показана пунктиром) уменьшается со временем по экспоненциальному закону.
Промежуток времени 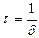 , в течение которого амплитуда
|
уменьшается в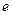 
раз, называется временем релаксации.
Период затухающих колебаний равен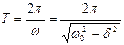 
, (1.8.17)
где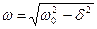 
– частота затухающих колебаний.
Показателем степени затухания колебаний является декремент затухания. Он равен отношению амплитуд, соответствующих моментам времени 
и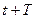 
, т.е.
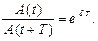(1.8.18)
Натуральный логарифм данного выражения называется логарифмическим декрементом затухания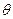 
: 
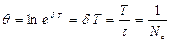, (1.8.19)
где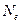 
– число колебаний, совершенных за время уменьшения амплитуды в 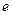раз.
