2014-02-02
546
Пусть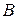 
ограничено сверху элементом 
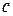, т.е. 
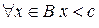. Рассмотрим множество 
. 
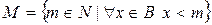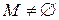, т.к. 
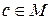. Тогда, по теореме 3, 
имеет наименьший элемент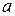 
, причем 
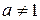, т. к. в противном случае 
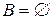. По следствию 4) из аксиом Пеано, 
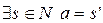. Предположим, что 
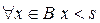, следовательно, 
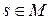. Последнее противоречит тому, что 
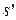- наименьший в , а, значит, предположение неверно. Тогда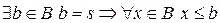 
. Таким образом, 
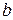- наибольший в .
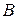что и требовалось доказать.
ІІ и ІІІ формы метода математической индукции для натуральных чисел.
Теорема 9 ( ІІ форма ): Если утверждение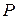 
о натуральных числах верно для 1 и для произвольного натурального числа 
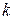, большего 1, из верности утверждения 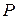для всех натуральных чисел, меньших 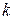, следует верность утверждения для числа 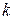, то утверждение верно для каждого натурального числа.
