2014-02-02
370
Предположим, что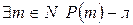 
. Рассмотрим множество 
. 
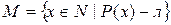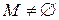, т.к. 
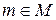. Также 
ограничено сверху любым элементом из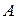 
. Тогда, по теореме 4, имеет наибольший элемент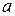 
, причем 
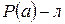. Рассмотрим элемент 
. 
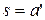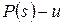, т.к. в противном случае, 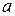не будет наибольшим в . Согласно индуктивному предположению,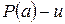 
, но это противоречит условию 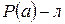. Таким образом, предположение неверно, и 
.
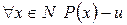что и требовалось доказать.
