Определение. Суммой последовательностей  и
и 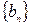 называется последовательность, полученная в результате сложения соответствующих членов этих последовательностей, т.е.
называется последовательность, полученная в результате сложения соответствующих членов этих последовательностей, т.е. 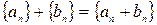 .
.
Определение. Произведением последовательностей  и
и 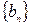 называется последовательность, полученная в результате умножения соответствующих членов этих последовательностей, т.е.
называется последовательность, полученная в результате умножения соответствующих членов этих последовательностей, т.е. 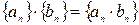 .
.
Замечание. Разностью последовательностей  и
и 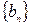 является сумма последовательностей
является сумма последовательностей  и
и 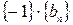 .
.
Теорема 2. Сумма, произведение и разность сходящихся последовательностей рациональных чисел является сходящейся последовательностью.
Доказательство.
Поскольку предел суммы, произведения, разности сходящихся последовательностей равен соответственно сумме, произведению, разности пределов этих последовательностей, теорему можно считать доказанной.
что и требовалось доказать.
Свойство 4 ф.п.р.ч. Сумма, произведение и разность фундаментальных последовательностей рациональных чисел является фундаментальной последовательностью.
Доказательство.
Докажем теорему сначала для фундаментальных последовательностей.
Пусть  и
и 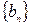 - фундаментальные последовательности рациональных чисел. Тогда
- фундаментальные последовательности рациональных чисел. Тогда 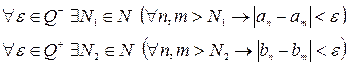 . Полагая
. Полагая 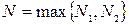 , получим
, получим 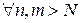
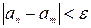 ,
, 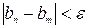 . Оценим
. Оценим 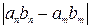 :
:
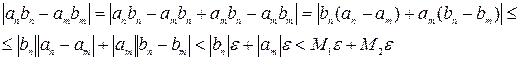 .
.
Последнее неравенство справедливо в силу свойства 3 ф.п.р.ч. оо ограниченности любой ф.п.р.ч.. Следовательно, последовательность 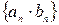 является фундаментальной.
является фундаментальной.
Аналогично устанавливается фундаментальность последовательности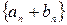 .
.
Последовательность 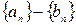 фундаментальна, поскольку
фундаментальна, поскольку 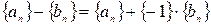 и всякая постоянная последовательность рациональных чисел фундаментальна
и всякая постоянная последовательность рациональных чисел фундаментальна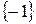 .
.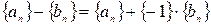 .
.
что и требовалось доказать
Определение. Частным двух последовательностей  и
и 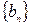 при условии, что среди членов последовательности
при условии, что среди членов последовательности 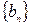 отсутствуют числа, равные нулю, называется последовательность
отсутствуют числа, равные нулю, называется последовательность 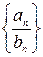 .
.
Свойство 5 ф.п.р.ч. Частным фундаментальных последовательностей  и
и 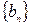 рациональных чисел при условии, что среди членов последовательности
рациональных чисел при условии, что среди членов последовательности 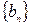 отсутствуют числа, равные нулю, и
отсутствуют числа, равные нулю, и 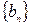 не сходится к нулю, является фундаментальной последовательностью рациональных чисел.
не сходится к нулю, является фундаментальной последовательностью рациональных чисел.
Доказательство.
Поскольку 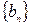 не сходится к нулю, то найдется положительное рациональное число
не сходится к нулю, то найдется положительное рациональное число 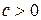 и натуральное
и натуральное 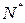 такие, что
такие, что 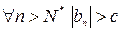 . Поскольку последовательности
. Поскольку последовательности  и
и 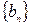 фундаментальны, имеем:
фундаментальны, имеем:
 - ограниченная, следовательно,
- ограниченная, следовательно, 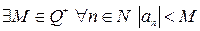 ;
;
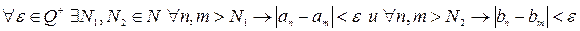 .
.
Выберем 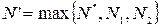 . Тогда
. Тогда
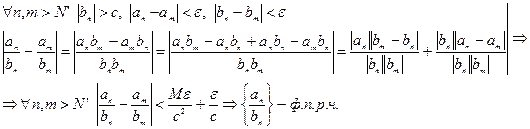
что и требовалось доказать
 2014-02-02
2014-02-02 521
521








