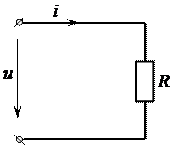 Пусть к зажимам цепи с активным сопротивлением R приложено напряжение источника питания
Пусть к зажимам цепи с активным сопротивлением R приложено напряжение источника питания 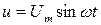 . Для простоты принимаем, что начальная фаза напряжения равна нулю, так как для установившегося режима начальная фаза не имеет никакого значения.
. Для простоты принимаем, что начальная фаза напряжения равна нулю, так как для установившегося режима начальная фаза не имеет никакого значения.
В соответствии со вторым законом Кирхгофа для мгновенных значений напряжения имеем  . Решая это уравнение относительно тока i и заменяя u на
. Решая это уравнение относительно тока i и заменяя u на  , получаем
, получаем
 ,
,
причем амплитуда тока в цепи
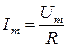 .
.
Из предыдущего уравнения видно, что ток в элементе с активным сопротивлением совпадает по фазе с напряжением на этом элементе.

Так как действующие значения напряжения и тока в 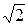 раза меньше их максимальных значений, то аналогично
раза меньше их максимальных значений, то аналогично 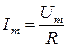 можно записать
можно записать 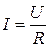 , то есть действующие значения синусоидальных напряжений и тока связаны между собой законом Ома так же, как постоянные ток и напряжение.
, то есть действующие значения синусоидальных напряжений и тока связаны между собой законом Ома так же, как постоянные ток и напряжение.
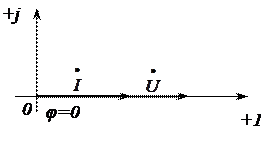 |
На векторной диаграмме комплексные значения напряжения  и тока
и тока 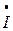 в цепи представлены векторами на комплексной плоскости. Начала векторов совмещены с началом координат, длины векторов в соответствующем масштабе равны действующим значениям напряжения и тока. Вещественная ось направлена горизонтально, а мнимая – вертикально. Начальный вектор совмещаем с положительным направлением вещественной оси. Для цепи с активным сопротивлением векторы напряжения и тока совпадают по направлению.
в цепи представлены векторами на комплексной плоскости. Начала векторов совмещены с началом координат, длины векторов в соответствующем масштабе равны действующим значениям напряжения и тока. Вещественная ось направлена горизонтально, а мнимая – вертикально. Начальный вектор совмещаем с положительным направлением вещественной оси. Для цепи с активным сопротивлением векторы напряжения и тока совпадают по направлению.
Мгновенное значение мощности цепи синусоидального тока равно произведению мгновенных значений напряжения и тока:
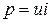 .
.
Если в цепь приложено напряжение 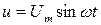 , то в общем случае ток в цепи
, то в общем случае ток в цепи 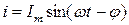 . Следовательно
. Следовательно
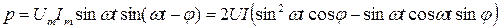
После преобразований получим

таким образом, мгновенное значение мощности имеет две составляющие: постоянную 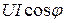 , не изменяющийся во времени, и переменную
, не изменяющийся во времени, и переменную 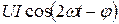 , изменяющийся периодически с частотой 2 ω. Вследствие этого мгновенное значение мощности также изменяется с двойной частотой.
, изменяющийся периодически с частотой 2 ω. Вследствие этого мгновенное значение мощности также изменяется с двойной частотой.
 |
При этом мощность положительна, если напряжение и ток совпадают по направлению, и отрицательна, если напряжение и ток имеют разные знаки. Когда мощность положительна, тогда электрическая энергия передается от источника к приемнику и наоборот.
Для количественной оценки электроэнергетических процессов удобнее использовать среднее значение мощности Pср, которое можно найти, вычислив работу, совершаемую за один период:
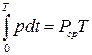
откуда

Так как 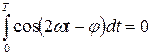 , то
, то 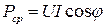 , то есть среднее значение мощности равно постоянной составляющей мгновенного значения мощности. Средняя мощность характеризует интенсивность передачи электроэнергии от источника к приемнику и её преобразования в другие виды энергии, то есть активный необратимый процесс. Поэтому среднюю мощность называют активной мощностью и выражают в ваттах, киловаттах, мегаваттах
, то есть среднее значение мощности равно постоянной составляющей мгновенного значения мощности. Средняя мощность характеризует интенсивность передачи электроэнергии от источника к приемнику и её преобразования в другие виды энергии, то есть активный необратимый процесс. Поэтому среднюю мощность называют активной мощностью и выражают в ваттах, киловаттах, мегаваттах
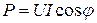 .
.
Активная мощность цепи синусоидального тока равна произведению действующих значений напряжения и тока и косинуса угла между их векторами.
Для цепи, состоящей из элемента только с активным сопротивлением R, φ =0 и
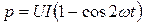 .
.
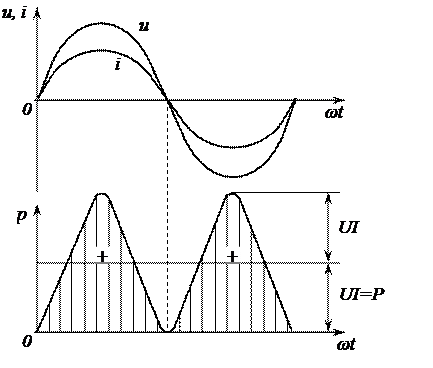 |
Напряжение и ток совпадают по фазе, и мгновенное значение мощности всегда положительно. Это указывает на то, что при наличии в цепи только элемента с активным сопротивлением вся электроэнергия преобразуется в тепловую или другие виды энергии. Среднее значение мощности или активная мощность 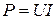 , так как
, так как 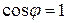 .
.
Поскольку напряжение на элементе с сопротивлением R 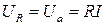 , активная мощность цепи может быть определена как
, активная мощность цепи может быть определена как
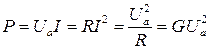 .
.
 2014-02-02
2014-02-02 5677
5677








