R, L, C – это параметры электрической цепи, причем активное сопротивление R характеризует активный (необратимый) процесс преобразования электрической энергии в другие виды энергии, а индуктивность L и емкость C – обратимый процесс преобразования энергии электромагнитного поля.

Под действием напряжения 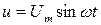 источника питания в цепи возникает ток i. Ток создает падения напряжения на элементах цепи:
источника питания в цепи возникает ток i. Ток создает падения напряжения на элементах цепи: 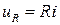 - на элементе с активным сопротивлением;
- на элементе с активным сопротивлением; 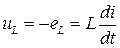 - на элементе с индуктивностью;
- на элементе с индуктивностью; 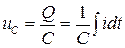 - на элементе с емкостью. По второму закону Кирхгофа для данной цепи запишем
- на элементе с емкостью. По второму закону Кирхгофа для данной цепи запишем
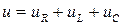 или
или 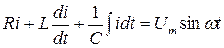
В результате решения данного уравнения найдем  .
.
Найдем частное решение данного уравнения, то есть ток установившегося режима. Так как правая часть этого уравнения – синусоидальная функция, то и частное решение следует искать в виде синусоидальной функции
 .
.
Функция  полностью определена, если известны амплитуда тока Im и угол сдвига фаз φ между напряжением и током. Найдем эти величины.
полностью определена, если известны амплитуда тока Im и угол сдвига фаз φ между напряжением и током. Найдем эти величины.
Как было показано ранее, напряжение 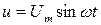 изображается комплексным числом
изображается комплексным числом  ; ток
; ток  - комплексным числом
- комплексным числом 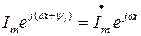 ; производная
; производная 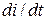 - комплексным числом
- комплексным числом 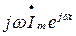 ; интеграл
; интеграл 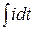 - комплексным числом
- комплексным числом 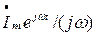 .
.
Перейдем от дифференциального уравнения к алгебраическому уравнению в комплексной форме
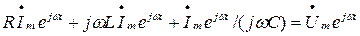 .
.
После преобразования имеем
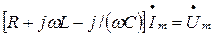
а разделив обе части уравнения на 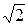 , получим аналогичное линейное алгебраическое уравнение для комплексных действующих значения:
, получим аналогичное линейное алгебраическое уравнение для комплексных действующих значения:
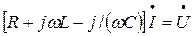
Коэффициент
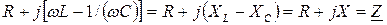
является полным сопротивлением цепи в комплексной форме. Вещественная составляющая R полного сопротивления равна активному сопротивлению цепи, а мнимая составляющая X называется её реактивным сопротивлением. Реактивное сопротивление цепи равно разности индуктивного и емкостного сопротивлений:
 .
.
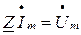 ;
; 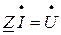 ,
,
откуда комплексное полное сопротивление
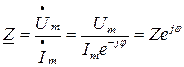 ,
,
где модуль полного сопротивления
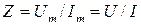 .
.
Таким образом, модуль полного сопротивления цепи равен отношению модулей действующих значений напряжения и тока, а аргумент комплексного сопротивления – сдвигу фаз φ между векторами напряжения и тока.
Модуль полного сопротивления цепи
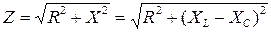
то есть, полное сопротивление цепи равно корню квадратному из суммы квадратов активного и реактивного сопротивлений.
Можем найти амплитуду тока, определяющую функцию 
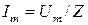 .
.
Теперь, если воспользоваться равенством
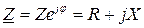 ,
,
можно определить угол сдвига фаз φ
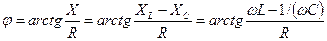 .
.
Таким образом, значение угла φ зависит от соотношения между реактивным X и активным R сопротивлениями. Чем больше реактивное сопротивление, тем больше угол φ. Знак угла φ зависит от соотношения между индуктивным и емкостным сопротивлениями. Если 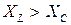 , то угол φ положительный и ток можно определить по формуле
, то угол φ положительный и ток можно определить по формуле  , откуда видно, что ток отстает по фазе от напряжения на угол φ. Если
, откуда видно, что ток отстает по фазе от напряжения на угол φ. Если 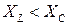 , то угол φ отрицательный и ток
, то угол φ отрицательный и ток 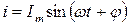 , то есть опережает по фазе напряжение на угол φ.
, то есть опережает по фазе напряжение на угол φ.
На рисунке показано, как изменяются напряжение и ток в цепи с последовательно соединенными активным, индуктивным и емкостным сопротивлениями при условии 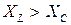 :
:
 |
При построении векторной диаграмм в качестве начального удобно выбрать вектор тока, так как при последовательном соединении ток во всех элементах один и тот же. Как было условлено, начальный вектор совмещаем с положительным направлением мнимой оси (здесь и далее оси обозначать не будем).
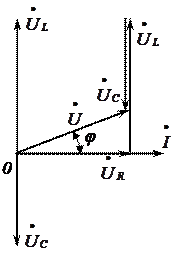
Падения напряжения в комплексной форме на участке цепи с активным, индуктивным и емкостным сопротивлениями соответственно
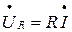 ;
;  ;
; 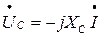 .
.
Вектор 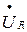 на участке с активным сопротивлением совпадает по фазе с вектором
на участке с активным сопротивлением совпадает по фазе с вектором 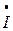 , и на векторной диаграмме его проводим в направлении тока. Падение напряжения
, и на векторной диаграмме его проводим в направлении тока. Падение напряжения 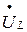 на участке с индуктивностью опережает ток по фазе на угол π /2, причем поворачивать вектор надо против часовой стрелки по отношению к вектору
на участке с индуктивностью опережает ток по фазе на угол π /2, причем поворачивать вектор надо против часовой стрелки по отношению к вектору 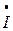 . Падение напряжения
. Падение напряжения  на участке с емкостью отстает от тока на угол π /2, причем
на участке с емкостью отстает от тока на угол π /2, причем  следует повернуть на угол 90º по направлению вращения часовой стрелки по отношению к вектору
следует повернуть на угол 90º по направлению вращения часовой стрелки по отношению к вектору 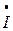 .
.
По второму закону Кирхгофа можно написать уравнение
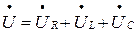 .
.
Для нахождения вектора  полного напряжения цепи к концу вектора
полного напряжения цепи к концу вектора 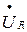 пристраиваем вектор
пристраиваем вектор 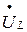 путем параллельного переноса, а к концу вектора
путем параллельного переноса, а к концу вектора 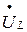 пристраиваем вектор
пристраиваем вектор  . Вектор полного напряжения
. Вектор полного напряжения  соединяет начало координат с концом вектора
соединяет начало координат с концом вектора  (последнего слагаемого вектора).
(последнего слагаемого вектора).
Поскольку векторная диаграмма построена для случая, когда 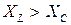 (следовательно, и
(следовательно, и 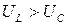 ), ток в цепи отстает по фазе на угол φ от полного напряжения, комплексное значение которого
), ток в цепи отстает по фазе на угол φ от полного напряжения, комплексное значение которого 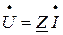 .
.
 2014-02-02
2014-02-02 3094
3094








