Индуктивностью L теоретически обладают все проводники с током. Но в некоторых случаях эта индуктивность так мала, что ею вполне можно пренебречь. Значительна индуктивность у обмоток или катушек, состоящих из большого числа витков провода.
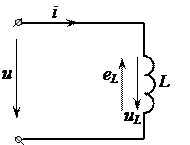 Рассмотрим идеальную катушку с постоянной индуктивностью L, то есть такую катушку, активное сопротивление которой равно нулю.
Рассмотрим идеальную катушку с постоянной индуктивностью L, то есть такую катушку, активное сопротивление которой равно нулю.
Пусть к цепи с индуктивностью L приложено синусоидальное напряжение 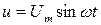 . Под действием этого напряжения в цепи индуктивной катушки возникает ток i. Этот ток создает магнитный поток Ф, который согласно закону электромагнитной индукции индуцирует в катушке ЭДС самоиндукции
. Под действием этого напряжения в цепи индуктивной катушки возникает ток i. Этот ток создает магнитный поток Ф, который согласно закону электромагнитной индукции индуцирует в катушке ЭДС самоиндукции
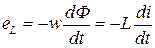
где w – число витков катушки.
Условное положительное направление ЭДС eL выбирают из условия, что её действительное направление в любой момент времени противоположно направлению uL (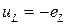 ).
).
По второму закону Кирхгофа имеем 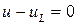 , а с учетом того, что
, а с учетом того, что 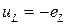 , получаем
, получаем
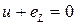 .
.
Чтобы получить это уравнение на основании 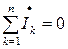 , условное положительное направление eL следует всегда принимать совпадающим с положительным направлением тока.
, условное положительное направление eL следует всегда принимать совпадающим с положительным направлением тока.
 или
или 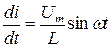
Решая это уравнение, получим выражение для тока в цепи:
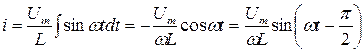
Так как амплитуда тока
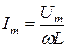
то окончательное выражение для тока имеет вид
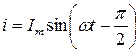 .
.
Видно, что в цепи с индуктивностью ток также изменяется по синусоидальному закону и отстает по фазе от напряжения на угол π/ 2.
 |
В формуле 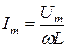 знаменатель
знаменатель 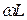 в правой части имеет размерность сопротивления. Это индуктивное сопротивление
в правой части имеет размерность сопротивления. Это индуктивное сопротивление
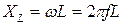 .
.
Индуктивное сопротивление прямо пропорционально частоте и индуктивности. С учетом этой формулы получаем
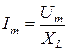 .
.
Для действующих значений напряжения и тока
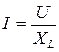 .
.
Так как согласно 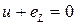 ЭДС самоиндукции численно равна напряжению на элементе с индуктивностью, то, используя
ЭДС самоиндукции численно равна напряжению на элементе с индуктивностью, то, используя 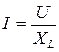 , имеем
, имеем
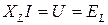 .
.
Видно, что индуктивное сопротивление является коэффициентом пропорциональности между током и ЭДС самоиндукции.
В соответствии с 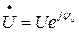 принимая во внимание, что
принимая во внимание, что 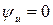 , комплексное напряжения
, комплексное напряжения 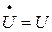 , а в соответствии с
, а в соответствии с 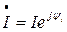 и
и 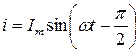 комплексный ток
комплексный ток
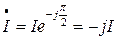 .
.
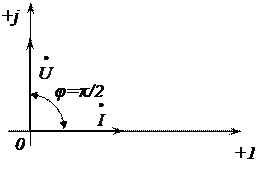 |
На векторной диаграмме вектор напряжения, имеющий начальную фазу, равную нулю, отложен по мнимой оси, а вектор тока, имеющий начальную фазу 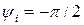 , - в положительном направлении вещественной оси. Угол сдвига фаз между напряжением и током в цепи с индуктивностью
, - в положительном направлении вещественной оси. Угол сдвига фаз между напряжением и током в цепи с индуктивностью 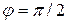 .
.
Если модули напряжения и тока связаны соотношением 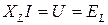 , то их комплексные значения связаны соотношением
, то их комплексные значения связаны соотношением
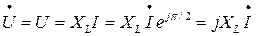 .
.
В цепи с индуктивностью L угол 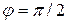 и формула
и формула  принимает вид
принимает вид
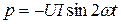 ,
,
 то есть мгновенное значение мощности имеет только переменную составляющую.
то есть мгновенное значение мощности имеет только переменную составляющую.
Первую четверть периода ток совпадает по направлению с ЭДС самоиндукции eL индуктивной катушки, мощность отрицательна и энергия передается от катушки к источнику питания. Вторую четверть периода ток совпадает по направлению с напряжением источника питания, мощность положительна, а энергия поступает от источника к приемнику (индуктивной катушке) и запасается в его магнитном поле. В течение третьей четверти периода ток опять совпадает по направлению с eL и запасенная в магнитном поле катушки энергия передается источнику питания (мощность отрицательна).
Таким образом, в течение одного периода электроэнергия дважды поступает от источника в катушку и обратно. При этом вся передаваемая энергия запасается в магнитном поле катушки и затем вся возвращается источнику. Такая энергия обмена между источником и приемником, которая не преобразуется в другие виды энергии, называется реактивной. Интенсивность обмена электроэнергией характеризуется реактивной мощностью QL, равной амплитуде мгновенного значения мощности, то есть
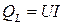
Реактивную мощность выражают в вольт-амперах реактивных (вар), киловольт-амперах реактивных (квар) и т.д.
Напряжение на элементе с индуктивностью 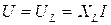 , поэтому реактивная мощность можно также определить по формулам
, поэтому реактивная мощность можно также определить по формулам
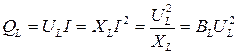 ,
,
где 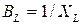 - индуктивная проводимость.
- индуктивная проводимость.
 2014-02-02
2014-02-02 6941
6941








