2014-02-02
353
| Основание q | Система счисления | Цифры (алфавит) |
| Двоичная | 0, 1 | |
| Троичная | 0, 2 | |
| ... | ... | ... |
| Восьмеричная | 0, 1, 2, 3, 4, 5, 6, 7 | |
| Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 | |
| Шестнадцатеричная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, В, С, D, E, F |
В позиционной системе счисления значительно легче производить арифметические операции, например, необходимо сложить числа 29,7 и 8,2.
В римской системе счисления (XXIX,VII + VIII,II) такую операцию провести достаточно трудно, если не сказать невозможно.
Компьютеры используют двоичную систему, так как она имеет ряд преимуществ:
1) для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток – нет тока, низкое или высокое напряжение);
2) представление информации посредством только двух состояний надежно и помехоустойчиво;
3) двоичная арифметика намного проще десятичной;
4) простота реализации процессов хранения, передачи и обработки информации на компьютере.
Недостаток двоичной системы – быстрый рост числа разрядов, необходимых для записи чисел [21].
Для обозначения адресов расположения данных в памяти компьютера и других целей удобнее пользоваться не двоичным и десятичным, а шестнадцатеричным представлением чисел.
3.2. Правила перевода из одной системы счисления
в другую
Перевод из десятичной системы счисления в любую другую
Для перевода из десятичной системы счисления в двоичную существует правило, которое годится для всех систем счисления.
Для того, чтобы перевести число из десятичной системы счисления в любую другую, надо делить число на основание системы счисления до тех пор, пока частное от деления не будет меньше основания системы счисления, при этом необходимо фиксировать все остатки от деления. Затем надо записать частное от деления и все остатки, начиная с последнего в обратной последовательности. Таким образом, получится: частное – старший разряд, а самый первый остаток – младший разряд.
Пример.
1. 
Целые числа
7510 = 10010112
2. Десятичные дроби
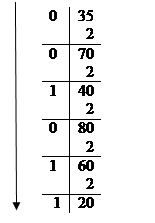0,3510 = 0,010112
Результат: 75,3510 = 1001011,010112
Перевод чисел с основанием,
отличным от 10 в десятичную систему счисления
Для перевода числа из системы счисления с любым основанием в десятичную необходимо каждую цифру этого числа умножить на его основание в степени, равной номеру разряда этой цифры в записи числа и полученные произведения сложить (разряды в записи числа нумеровать справа налево, начиная с нуля).
