Методы принятия решений. Практически любой метод принятия решений, используемый в управлении, можно технически рассматривать как разновидность моделирования

Практически любой метод принятия решений, используемый в управлении, можно технически рассматривать как разновидность моделирования. Однако по традиции термин «модель» обычно относится лишь к методам общего характера, только что описанным выше, а также к многочисленным их специфическим разновидностям. В дополнение к моделированию, имеется ряд методов, способных оказать помощь ру­ководителю в поиске объективно обоснованного решения по выбору из нескольких альтернатив той, которая в наибольшей мере способствует достижению целей. Под заголовок данного раздела попадают платежная матрица и дерево решений, описан­ные ниже. Для облегчения использования этих методов и вообще повышения каче­ства принимаемых решений руководство пользуется прогнозированием. Наиболее распространенные методы прогнозирования рассмотрены в следующем разделе. На­ша цель заключается в том, чтобы помочь понять суть этих инструментов, а не научить ими пользоваться.

Платежная матрица. Суть каждого принимаемого руководством решения — выбор наилуч­шей из нескольких альтернатив по конкретным установленным зара­нее критериям. (Если вы захотите вспомнить рассмотрение ограничений и критериев для принятия решений, обратитесь к гл. 6). Платежная матрица — это один из методов статистической теории решений, метод, который может оказать помощь руководителю в выборе одного из нескольких вариантов. Он особенно полезен, когда руководитель должен установить, какая стратегия в наибольшей мерс будет способ­ствовать достижению целей.

По словам Н. Пола Лумбы: «Платеж представляет собой денежное вознагражде­ние или полезность, являющиеся следствием конкретной стратегии в сочетании с конкретными обстоятельствами. Если платежи представить в форме таблицы (или матрицы), мы получаем платежную матрицу»²⁴, как показано на рис. 8.4. Слова «в сочетании с конкретными обстоятельствами» очень важны, чтобы понять, когда мож­но использовать платежную матрицу и оценить, когда решение, принятое на ее основе, скорее всего будет надежным. В самом общем виде матрица означает, что платеж зависит от определенных событий, которые фактически свершаются. Если такое событие или состояние природы не случается на деле, платеж неизбежно будет иным.

В целом платежная матрица полезна, когда:

1. Имеется разумно ограниченное число альтернатив или вариантов стратегии для выбора между ними.

2. То, что может случиться, с полной определенностью не известно.

3. Результаты п ринятого решения зависят от того, какая именно выбрана альтерна­тива и какие события в действительности имеют место.

Кроме того, руководитель должен располагать возможностью объективной оцен­ки вероятности релевантных событий и расчета ожидаемого значения такой вероят­ности. Руководитель редко имеет полную определенность. Но также редко он действует в условиях полной неопределенности. Почти во всех случаях принятия решений руководителю приходится оценивать вероятность или возможность собы­тия. Из предшествующего рассмотрения напомним, что вероятность варьирует от 1, когда событие определенно произойдет, до 0, когда событие определенно не произой­дет. Вероятность можно определить объективно, как поступает игрок в рулетку, ставя на нечетные номера. Выбор ее значения может опираться на прошлые тенденции или субъективную оценку руководителя, который исходит из собственного опыта дейст­вий в подобных ситуациях.

Если вероятность не была принята ъ расчет, решение всегда будет соскальзывать в направлении наиболее оптимистических последствий. Например, если исходить из того, что инвесторы на удачной кинокартине могут иметь 500% на инвестированный капитал, а при вложении в торговую сеть — в самом благоприятном варианте всего 20%, то решение всегда должно быть в пользу кинопроизводства. Однако если взять в расчет, что вероятность большого успеха кинофильма весьма невысока, капиталов­ложения в магазины становятся более привлекательными, поскольку вероятность получения указанных 20% очень значительна. Если взять более простой пример, то выплаты при ставках в заезде на длинную дистанцию на скачках выше, поскольку выше вероятность, что не выиграешь вообще ничего.

Вероятность прямо влияет на определение ожидаемого значения — центральной концепции платежной матрицы. Ожидаемое значение альтернативы или варианта стратегии — это сумма возможных значений, умноженных на соответствующие вероятности. К примеру, если вы считаете, что вложение средств (как стратегия действий) в киоск для торговли мороженым с вероятностью 0,5 обеспечит вам годовую прибыль 5000 долл., с вероятностью 0,2 — 10 000 долл. и с вероятностью 0,3 — 3000 долл., то ожидаемое значение составит:

5000 (0,5) + 10 000 (0,2) + 3000 (03) = 5400 долл.

Определив ожидаемое значение каждой альтернативы и расположив результаты в виде матрицы, руководитель без труда может установить, какой выбор наиболее привлекателен при заданных критериях. Он будет, конечно, соответствовать наивыс­шему ожидаемому значению. Исследования показывают: когда установлены точные значения вероятности, методы дерева решений и платежной матрицы обеспечивают принятие более качественных решений, чем традиционные подходы.

____ Дерево решений. Дерево решений — еще один популярный метод науки управления, используемый для выбора наилучшего направления действий из име­ющихся вариантов. «ДЕРЕВО РЕШЕНИЙ — это схематичное представление проб­лемы принятия решений». Как и платежная матрица, дерево решений дает руководителю возможность «учесть различные направления действий, соотнести с ними финансовые результаты, скорректировать их в соответствии с приписанной им вероятностью, а затем сравнить альтернативы». Концепция ожидаемого значения является неотъемлемой частью метода дерева решений.

Методом дерева решений можно пользоваться в ситуациях, подобных описанной выше, в связи с рассмотрением платежной матрицы. В этом случае предполагается, что данные о результатах, вероятности и т.п. не влияют на все последующие решения. Однако дерево решений можно построить под более сложную ситуацию, когда ре­зультаты одного решения влияют на последующие решения. Таким образом, дерево решений — это полезный инструмент для принятия последовательных решений.

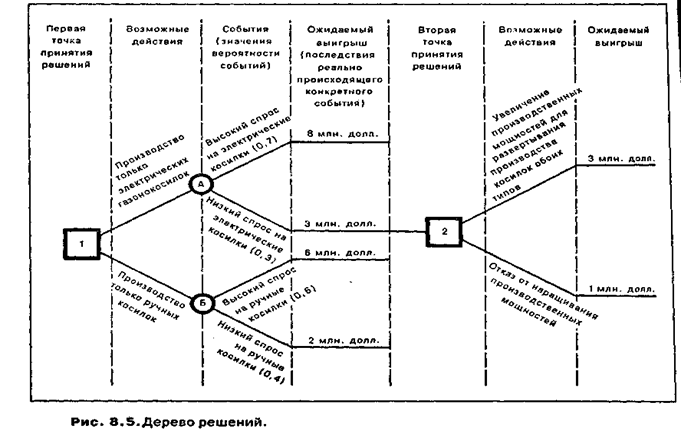
На рис. 8.5. проиллюстрировано применение метода дерева решений для разреше­ния проблемы, требующей определенной последовательности решений. Вице-прези­дент по производству из компании, в настоящее время выпускающей электрические газонокосилки, считает, что расширяется рынок ручных косилок. Он должен решить, стоит ли переходить на производство ручных косилок, и если сделать это, — стоит или не стоит продолжать выпуск электрических газонокосилок. Производство коси­лок обоих типов потребует увеличения производственных мощностей. До принятия решения руководитель собрал релевантную информацию об ожидаемых выигрышах в случае тех или иных вариантов действий и о вероятности соответствующих собы­тий. Эта информация представлена на дереве решений.

Используя дерево решений, руководитель находит путем возврата от второй точки к началу наиболее предпочтительное решение — наращивание производствен­ных мощностей под выпуск косилок обоих типов. Это обусловлено ожидаемым выиг­рышем (3 млн. долл.), который превышает выигрыш (1 млн. долл.) при отказе от такого наращивания, если в точке А будет низкий спрос на электрические косилки.

Руководитель продолжает двигаться назад к текущему моменту (первой точке принятия решений) и рассчитывает ожидаемые значения в случаях альтернативных действий — производства только электрических или только ручных косилок. Ожи­даемое значение для варианта производства только электрических косилок состав­ляет 6,5 млн. долл. (0,7 х 8 млн. долл. + 0,3 х 3 млн. долл.). Подобным образом рассчитывается ожидаемое значение для варианта выпуска только ручных косилок, которое равно всего 4,4 млн. долл. Таким образом, наращивание производственных мощностей под выпуск косилок обоих типов является наиболее желательным реше­нием, поскольку ожидаемый выигрыш здесь наибольший, если события пойдут, как предполагается.