2014-02-02
1361
Как правило, выходным устройством источника информации, представленной в коде Грея, является матрица следующего вида:
 |
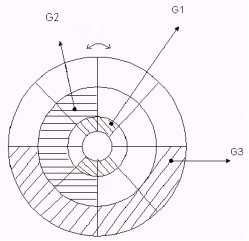Код Грея называют циклическим двоичным кодом и относят к непозиционным кодам, так как значение любого числа отличается от предыдущего или последующего только значением символа в одном из разрядов. Рассмотрим трехсимвольный код Грея:
| Циклический код Грея | Простой двоичный код | Эквива- лент | ||||
| G3 | G2 | G1 | B3 | B2 | B1 | |
Синтезировать преобразователь кода Грея в двоичный код с использованием элементной базы М2. Используем метод матриц для получения зависимостей Вi= F(Gi, Вi+1).
| G3, G2 | |||||
| 00 01 11 10 | |||||
| G1 | |||||
B3=G3
| G3, G2 | ||||||
| 00 01 11 10 | ||||||
| G1 | ||||||
|
|
|
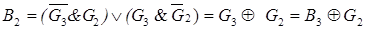
| G3, G2 | |||||
| 00 01 11 10 | |||||
| G1 | |||||
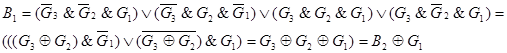
Принимая во внимание пункты 1,2,3, возможно для произвольного i-го разряда простого двоичного кода записать соотношение:
 |
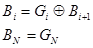Эти выражения являются аппаратной реализацией кода Грея.
Аппаратные затраты на синтезируемый преобразователь определяются разрядностью исходного кода.
 | |||
 | |||
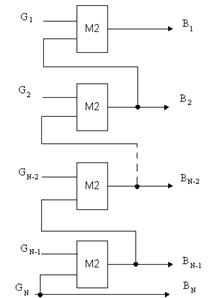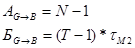N – число разрядов
Минимальные аппаратные затраты приводят к тому что время преобразования входного кода не отвечает режиму реального времени.
