Построение кривых переходного процесса
Теоретически кривая переходного процесса получается при решении дифференциального уравнения операторным методом, путем отыскания оригинала выходного сигнала при заданном типовом воздействии. График решения дифференциального уравнения и является кривой переходного процесса.
В курсе рассматриваются следующие методы построения кривой переходного процесса:
- метод трапецеидальных вещественных частотных характеристик (самостоятельно);
- на основе разностных уравнений.
Построение кривой переходного процесса на основе разностных уравнений предполагает дискретизацию непрерывных (аналоговых) уравнений.
Процесс дискретизации можно представить в виде работы следующего элемента (ключа) (рис. 5.9), где D t – шаг дискретизации.
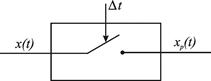
Рис. 5.9. Схема дискретизации переменной
Пусть x (t) – входной сигнал элемента представляет собой решение дифференциального или интегро-дифференциального уравнения (рис. 5.10а). На выходе ключа имеем сигнал xp(t), представленный на рис. 5.10б, т.е. последовательность импульсов длительностью h, где h – время замыкания ключа. Если h <<D t, то временем замыкания ключа можно пренебречь, что показано на рис. 5.10в.
Математически этот сигнал записывается в виде:
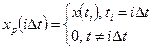 . (5.16)
. (5.16)
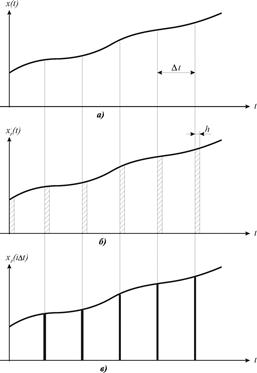
Рис. 5.10. Процесс дискретизации сигнала
и называется такой сигнал дискретным или решетчатым. Время ti=i D t называется дискретным временем. Если шаг дискретизации постоянный (Dt=const), то вместо дискретного времени ti=iDt используют аналог дискретного времени i, представляющий собой целое число. Тогда дискретный сигнал записывается в виде x (i), т.е.
x (i)= xр (iDt). (5.17)
Для получения дискретного сигнала x (i) на основе непрерывного x (t), представляющего собой решение дифференциального или интегро-дифференциального уравнения, достаточно последний дискретизировать с шагом D t в соответствии с выражением (5.17). Например:
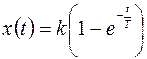 , то
, то 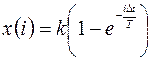 .
.
Дискретный сигнал x (i) можно получить и путем дискретизации непрерывных (дифференциальных или интегро-дифференциальных) уравнений, т.е. путем перехода к разностным уравнениям. Для получения разностного уравнения достаточно любую дискретную функцию, зависящую от другой дискретной функции представить в рекуррентной форме.
Линейное разностное уравнение n -го порядка записывается в виде:
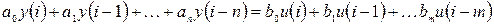 , (5.18)
, (5.18)
где i – аналог дискретного времени; a0, a1,…,an, b0, b1,…,bm – коэффициенты разностного уравнения.
Выразив y (i) из уравнения (5.18), получим рекуррентную формулу вида:
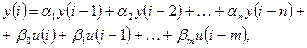 (5.19)
(5.19)
где
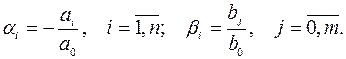
 2014-02-02
2014-02-02 1959
1959
