Получение разностного уравнения на основе интегрального уравнения

Пусть интегральное уравнение имеет вид:

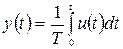. (5.20)

По определению интеграл представляет собой площадь криволинейной трапеции (рис. 5.11). При использовании метода прямоугольников для численного интегрирования получаем следующую сумму

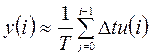, (5.21)

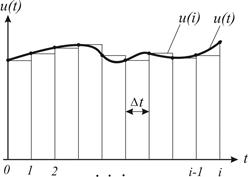
Рис.5.11. Дискретизация интегрального уравнения методом прямоугольников

т.е. площадь криволинейной трапеции заменяется приближенно суммарной площадью прямоугольников с основанием D t и высотой u (i). Тогда для i -1-го шага, т.е. предыдущего отчета имеем:

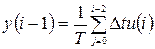. (5.22)

Вычтя выражение (5.22) из (5.21) получим уравнение вида:

,

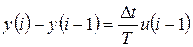т.е. разностное уравнение вида:

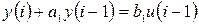, (5.23)

где а₁ =-1; b₁ =D t /T.

Отсюда

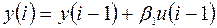, (5.24)

где b₁=b₁.