Теор. Общее ур-е прямой
В прямоуг. Декартовых координатах каждая прямая определяется ур-ем 1степени Ах+Ву+С=0 (*)
Ур-е (*) при произвольных А,В,С А,В≠0 одовременно определяют некоторую прямую.
Док-во
Если прямая не ║Оу то у=Кх+в или Кх-у+в=0 А=К В=-1 С=в
Если прямая ║Оу то х=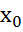 или х-
или х-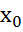 =0 А=1 В=0 С=-
=0 А=1 В=0 С=-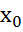
Обратное утв. Ах+Ву+С=0 Если В≠0, то у=
у=Кх+в К=-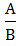 в=-
в=-  Если В=0, то А≠0 х=-
Если В=0, то А≠0 х=-  х=
х=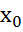
Опр1. Ур-е вида Ах+Ву+С=0 наз общим ур-ем прямой
Теор. N(A,B), координаты которого являются коэф. Перед х,у в общем ур-е прямой Ах+Ву+С=0, ┴ прямой опред. этим ур-ем.
Док-во.
 Ах+Ву+С=0
Ах+Ву+С=0
А +В
+В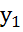 +С=0 _ N(A,B)┴
+С=0 _ N(A,B)┴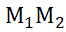 =
= )
)
А  +В
+В 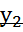 +С=0
+С=0
 =0
=0
Опр2. N=(A,B)наз нормальный вектор прямой Ах+Ву+С=0, а единичный вектор n=-  наз нормаль. Нормальный вектор позволяет опред. расположение А
наз нормаль. Нормальный вектор позволяет опред. расположение А +В
+В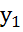 +С=0 и А
+С=0 и А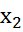 +В
+В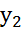 +С=0
+С=0
1)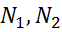 не коллинеарны, то прямые пересекаются
не коллинеарны, то прямые пересекаются
2) отрогональны(┴), то прямые
отрогональны(┴), то прямые 
3) коллинеарны, т.е
коллинеарны, т.е  , а
, а  ≠К
≠К , то прямые ║
, то прямые ║
 , т.е
, т.е  , а
, а  =К
=К , то прямые совп.
, то прямые совп.
Пр.а)через  (1;2) провести прямую ┴2х+3у+5=0
(1;2) провести прямую ┴2х+3у+5=0
 б) через
б) через  (1;2) провести прямую ║2х+3у+5=0 М(х,у)
(1;2) провести прямую ║2х+3у+5=0 М(х,у)
 а)
а) М ║N
М ║N

 a
a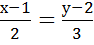

 a 3х-2у+1=0
a 3х-2у+1=0
б)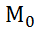 М ┴N a(
М ┴N a( М;N) =0
М;N) =0 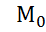 М(х-1;у-2)a2(х-1)+3(у-2)=0
М(х-1;у-2)a2(х-1)+3(у-2)=0
2х+3у-8=0
Угол между прямой и плоскостью.
А +В
+В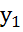 +С=0 и А
+С=0 и А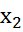 +В
+В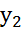 +С 𝞿=?
+С 𝞿=?
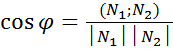 =
= чтоб ⦟=90
чтоб ⦟=90 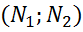 =
=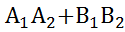 =0
=0
у=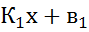 у=
у=
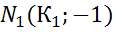
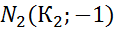
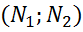 =
=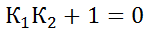
 - условие┴прямых
- условие┴прямых
 22.Нормальное ур-е прямой, расстояние от т. до прямой.
22.Нормальное ур-е прямой, расстояние от т. до прямой.
 1)АВ=(х-р
1)АВ=(х-р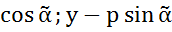 )
)
n=(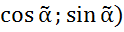 АВ┴n a(AB;n)=0
АВ┴n a(AB;n)=0
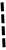
 (х-р
(х-р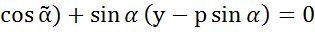

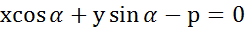 - нормальное ур-е прямой.
- нормальное ур-е прямой.
Ах+Ву+С=0 N=(A,B)a n=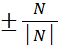 =(
=( )=(
)=(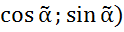
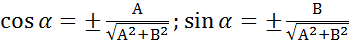
Ах+Ву+С=0 │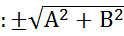
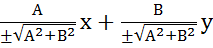
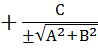 =0(чтоб перед р был знак -)
=0(чтоб перед р был знак -)
2)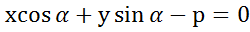
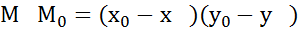
n=(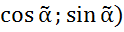
d=│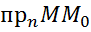 │=│(
│=│(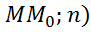 │=│
│=│ │
│
d=│ │
│
 прим.Найти расстояние от
прим.Найти расстояние от  до прямой 3х-4у+10=0
до прямой 3х-4у+10=0


 3х-4у+10=0│:(-
3х-4у+10=0│:(- )
)
-3х/5+4у/5-2=0
d=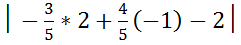 =4
=4
 23.Плоскости
23.Плоскости
Ах+Ву+Cz+D=0 N=(A,B,C) n=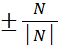 - нормаль
- нормаль
1)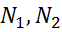 не коллинеарны, то пл-ти пересекаются по прямой
не коллинеарны, то пл-ти пересекаются по прямой
2) отрогональны(┴), то пл-ти
отрогональны(┴), то пл-ти 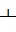
3) коллинеарны, т.е
коллинеарны, т.е  , а
, а 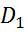 ≠К
≠К , то пл-ти ║
, то пл-ти ║
 т.е
т.е  , а
, а 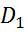 =К
=К , то пл-ти совп.
, то пл-ти совп.
Угол 𝞿 между плос-тями: 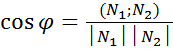 =
=
Условие┴пл-тей: 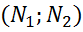 =
= =0
=0
Ур-е пл-ти в отрезках на осях(а,в,с) 
 2014-02-02
2014-02-02 1421
1421








