Абсолютная величина действительного числа
Модулем или абсолютной величиной действительного числа наз само число если оно >0или противоположное ему если <0
 │а│=
│а│=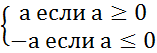
 │х│
│х│
 │х│
│х│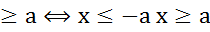
Теор о модуле суммы
Модуль суммы нескольких слагаемых 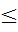 суммы модулей этих же слагаемых.
суммы модулей этих же слагаемых.
Док-во
 -│х│
-│х│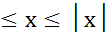
 -│у│
-│у│ 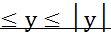
-(│х│+│у│)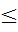 х+у
х+у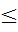 │х│+│у│
│х│+│у│  чтд
чтд
1)Сигментом 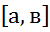 в мн-ве действительных чисел назовем мн-во
в мн-ве действительных чисел назовем мн-во 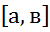 =
=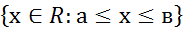
2)Интервал (а,в) в мн-ве действительных чисел назовем мн-во (а,в)=
3)Полуинтервалом [a,b),(a,b] в мн-ве действительных чисел назовем мн-во [a,b)= (a,b]
(a,b]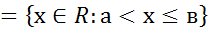
4)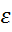 -окрестностью т.а в мн-ве действительных чисел наз интервал (а-
-окрестностью т.а в мн-ве действительных чисел наз интервал (а-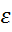 ,а+
,а+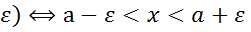 или │х-а│<
или │х-а│<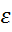
5)Рассматривая систему действительных чисел сост из мн-ва действительных чисел 𝑅 к которому присоед. 2 несобственных числа 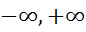 причем для них выполняются св-ва:
причем для них выполняются св-ва:
а)Если х-действительное число то -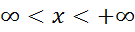 ; x+
; x+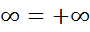
x- ;
; 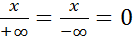
б)Если х>0 х(+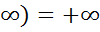 ; х(-
; х(-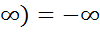
в)Если х<0 х(+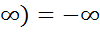 ; х(+
; х(+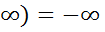 при этом любое действительное число – конечное; а несобственное число-бесконечное.
при этом любое действительное число – конечное; а несобственное число-бесконечное.
 2014-02-02
2014-02-02 527
527








