Прежде всего отметим, что векторный потенциал 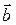 соленоидального поля
соленоидального поля  определяется с точностью до градиента произвольной функции.
определяется с точностью до градиента произвольной функции.
Действительно, так как поле 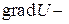 потенциально, то
потенциально, то 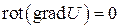 и потому
и потому
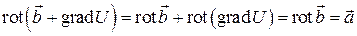 ;
;
значит, вектор 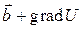 также является векторным потенциалом поля
также является векторным потенциалом поля  . Поэтому подбором вектора
. Поэтому подбором вектора 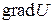 можно добиться того, чтобы одна из координат векторного потенциала
можно добиться того, чтобы одна из координат векторного потенциала 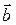 равнялась нулю, т.е. можно искать векторный потенциал, например, в виде
равнялась нулю, т.е. можно искать векторный потенциал, например, в виде 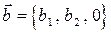 . Тогда
. Тогда
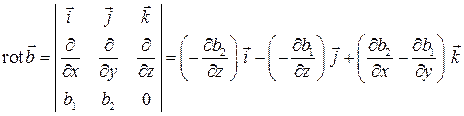 .
.
Так как 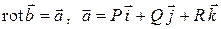 , то получим систему уравнений
, то получим систему уравнений
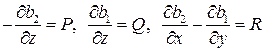 .
.
Проинтегрируем первое и второе из равенств по 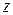 :
:
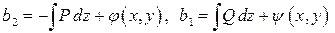 ;
;
здесь 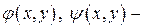 произвольные функции, не зависящие от переменной интегрирования
произвольные функции, не зависящие от переменной интегрирования 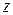 . Подставляя найденные
. Подставляя найденные 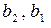 в третье из равенств, найдем функции
в третье из равенств, найдем функции 
Пример 2. Проверить соленоидальность поля 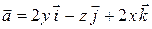 и найти его векторный потенциал.
и найти его векторный потенциал.
Решение. Так как 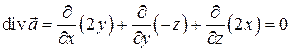 , то поле соленоидально, т.е.
, то поле соленоидально, т.е. 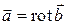 . Будем искать векторный потенциал в виде
. Будем искать векторный потенциал в виде 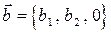 . Тогда
. Тогда
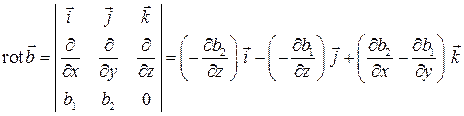 .
.
Так как 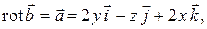 то получим систему уравнений
то получим систему уравнений
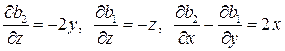 .
.
Проинтегрируем первое и второе из этих равенств по 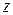 :
:
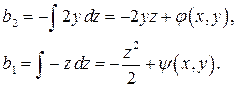
Подставив эти выражения для 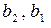 в третье из равенств, получим
в третье из равенств, получим
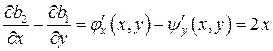 .
.
В частности, можно взять 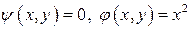 . Тогда векторный потенциал
. Тогда векторный потенциал
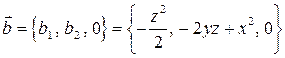 .
.
 2014-02-02
2014-02-02 2074
2074
