2014-02-02
1877
1). Поле 
является потенциальным с потенциалом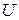 
тогда и только тогда, когда 
.
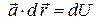2). Односвязное поле потенциально тогда и только тогда, когда в каждой точке поля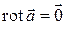 
.
3). В потенциальном поле линейный интеграл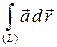 
не зависит от формы пути.
4). В потенциальном поле циркуляция по любому контуру, не охватывающему особых точек поля, равна нулю.
5). В потенциальном поле циркуляции по контурам, охватывающим все особые точки поля, равны между собой.
6). В потенциальном поле линейный интеграл по дуге равен разности потенциалов конца и начала дуги.
Пусть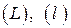 
─ контуры, окружающие все особые точки 
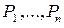поля; ориентируем контуры так, чтобы при обходе ограниченная ими область 
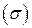оставалась слева, т.е. 
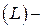против часовой стрелки, 
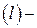по часовой стрелке; контуры с такой ориентацией обозначим соответственно 
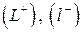. На поверхности 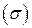с границей 
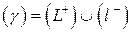поле потенциально, и потому 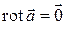по свойству 3) и теореме. Тогда по формуле Стокса
.
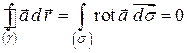С другой стороны,
,
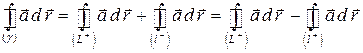и, следовательно,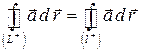 
.
6). Если поле потенциально и 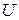─ его потенциал, то 
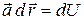и по формуле
.
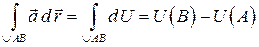В силовом потенциальном поле свойства 3 и 6 означают, что работа сил поля по дуге не зависит от формы дуги и равна разности потенциалов конца и начала дуги.
Рассмотрим способы отыскания потенциала 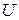поля .
Отыскание потенциала по выражению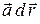 
Воспользуемся первым свойством потенциального поля. Если удается представить выражение 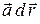в виде полного дифференциала некоторой функции 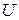, то поле ─ потенциально, а 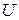─ его потенциал.
Пример 1. Показать, что поле потенциально и найти его потенциал, если
.
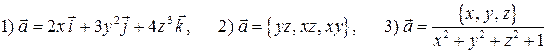Решение
1). 
.
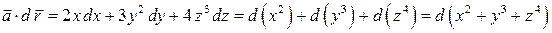Следовательно, поле ─ потенциально;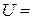 
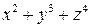─ его потенциал.
2). 
.
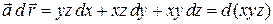Следовательно, поле потенциально;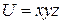 
─ его потенциал.
3). 
.
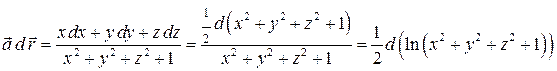Следовательно, поле ─ потенциально; 
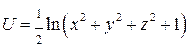─ его потенциал.
