Гармонические поля
Скалярное поле 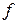 называется гармоническим, если функция
называется гармоническим, если функция 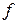 удовлетворяет уравнению Лапласа
удовлетворяет уравнению Лапласа
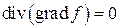 .
.
Правая часть уравнения Лапласа называется оператором Лапласа и обозначается  . Оператор Лапласа будет использован в дальнейшем при решении задач математической физики (задач колебания, теплопроводности, диффузии).
. Оператор Лапласа будет использован в дальнейшем при решении задач математической физики (задач колебания, теплопроводности, диффузии).
В прямоугольной системе координат
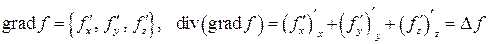
и уравнение Лапласа примет вид
 .
.
Пример 1. Показать, что поле 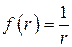 является гармоническим в пространстве
является гармоническим в пространстве 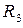 , а поле
, а поле 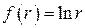 является гармоническим в пространстве
является гармоническим в пространстве 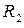 .
.
Решение. 1). По свойствам градиента 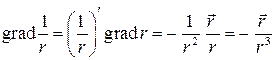 .
.
По свойствам дивергенции 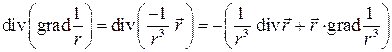 .
.
Учитывая, что 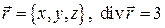 в пространстве
в пространстве  ,
, 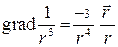 , получим:
, получим:
 .
.
2). В пространстве  для поля
для поля 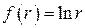 имеем:
имеем:
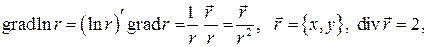
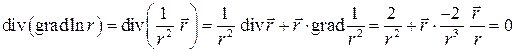 .
.
 2014-02-02
2014-02-02 2230
2230








