2014-02-02
803
Для потенциального поля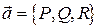 
и его потенциала 
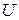имеем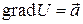 
или в координатной форме
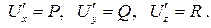
Проинтегрируем первое из этих равенств по 
; при этом появится константа, не зависящая от переменной интегрирования (но зависящая от 
):
.
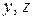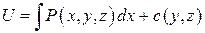Для отыскания функции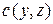 
следует подставить получившуюся функцию 
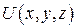во второе и третье равенства.
Пример 2. Проверить, что поле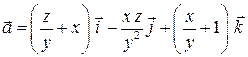 
является потенциальным и найти его потенциал.
Решение. Для данного поля проверить его потенциальность и найти потенциал по выражению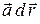 
сложно. Поэтому потенциальность поля проверим по условию 
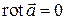, а потенциал найдем исходя из формул. Итак, вычислим ротор:
.
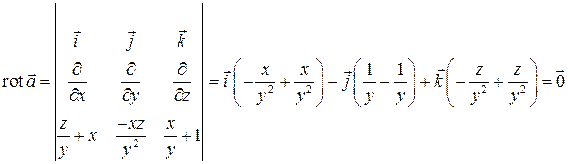Значит поле 
потенциально и его потенциал 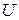удовлетворяет условию 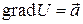или в координатной форме
Проинтегрируем первое из этих равенств по
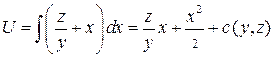
и подставим получившуюся функцию 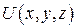во второе и третье равенства:
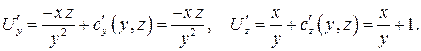
Отсюда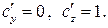 
Следовательно, 
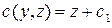, где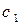 
─ константа. Поэтому
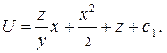
Отыскание потенциала центрального поля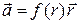 
Воспользуемся соотношением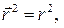 
где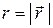 
. Тогда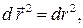 
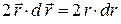и, значит, 
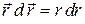. Поэтому
.
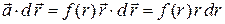Введем функцию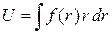 
. Так как 
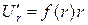, то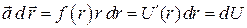 
. Следовательно, по свойству 1
центральное поле 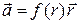потенциально и его потенциал .
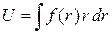Пример 3. Найти потенциал поля напряженностей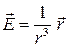 
.
Решение. Поле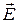 
─ центральное, следовательно, оно потенциальное, и его потенциал 
.
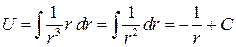17. Лекционное занятие. СОЛЕНОИДАЛЬНОЕ ПОЛЕ
Поле называют соленоидальным, если оно является полем ротора некоторой векторной функции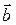 
, т.е. 
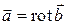; при этом вектор 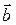называют векторным потенциалом поля .
