Повторные операции теории поля

1). Рассмотрим скалярное поле 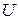. В нем определен вектор .

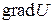В векторном поле 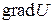определены понятия дивергенции и ротора

.

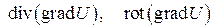2). Рассмотрим векторное поле . В нем определены скаляр 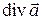и вектор 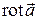. Для скалярного поля 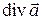определено понятие градиента

.

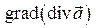Для векторного поля 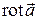определены понятия дивергенции и ротора

, .

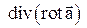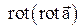Рассмотрим каждую из этих операций более подробно.

Выражение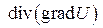есть оператор Лапласа ;

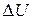Так как поле 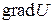является потенциальным, а в потенциальном поле ротор равен нулю, то .

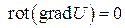Так как поле 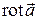является соленоидальным, а в соленоидальном поле дивергенция равна нулю, то .

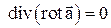Выражения 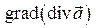и 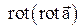используются в электродинамике и связаны соотношением (которое будет установлено позже)

.

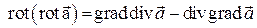Здесь 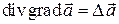для вектора 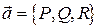понимают как

Учебное электронное текстовое издание

БЕЛОУСОВА ВЕРОНИКА ИГОРЕВНА