Оценка значимости уравнения регрессии и линейного
Оценка значимости всего уравнения регрессии в целом осуществляется с помощью  -критерия Фишера.
-критерия Фишера.
 -критерий Фишера заключается в проверке гипотезы о статистической значимости уравнения регрессии. Для этого выполняется сравнение фактического
-критерий Фишера заключается в проверке гипотезы о статистической значимости уравнения регрессии. Для этого выполняется сравнение фактического 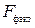 и критического (табличного)
и критического (табличного) 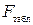 значений
значений  -критерия Фишера.
-критерия Фишера.
Значение 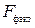 определяется из соотношения
определяется из соотношения
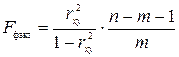 , ,
| (1.5) |
где 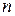 – число наблюдений;
– число наблюдений; 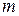 – число параметров при переменных (для линейной регрессии
– число параметров при переменных (для линейной регрессии  ).
).
Значение 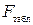 – максимально возможное значение критерия под влиянием случайных факторов при степенях свободы
– максимально возможное значение критерия под влиянием случайных факторов при степенях свободы 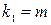 ,
, 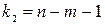 и уровне значимости
и уровне значимости 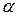 .
.
Уровень значимости 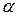 – вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно величина
– вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно величина 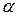 принимается равной 0,05.
принимается равной 0,05.
Если 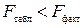 , то признается статистическая значимость и надежность оцениваемых характеристик. Если
, то признается статистическая значимость и надежность оцениваемых характеристик. Если 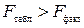 , то признается статистическая незначимость, ненадежность уравнения регрессии.
, то признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки статистической значимости линейного коэффициента парной корреляции 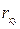 применяется
применяется 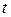 -критерий Стьюдента. Согласно
-критерий Стьюдента. Согласно 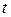 -критерию Стьюдента рассчитываются и сравниваются фактическое значение критерия
-критерию Стьюдента рассчитываются и сравниваются фактическое значение критерия 
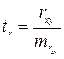 , где , где 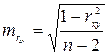
| (1.6) |
и критическое (табличное) значение  – максимально возможное значение критерия под влиянием случайных факторов при
– максимально возможное значение критерия под влиянием случайных факторов при 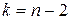 и уровне значимости
и уровне значимости 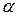 .
.
Если  , то линейный коэффициент парной корреляции статистически значим. Если
, то линейный коэффициент парной корреляции статистически значим. Если 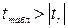 , то признается случайная природа формирования
, то признается случайная природа формирования 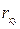 .
.
 2014-02-02
2014-02-02 442
442








