Оценка тесноты связи
Тесноту связи изучаемых явлений для линейной регрессии оценивает линейный коэффициент парной корреляции
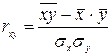 или или 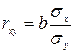 , ,
| (1.3) |
где 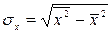 ,
, 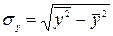 .
.
| 1о | Коэффициент 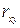 принимает значения на отрезке принимает значения на отрезке 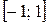 , т.е. , т.е. 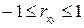 . Чем ближе . Чем ближе  к 1, тем теснее связь. к 1, тем теснее связь.
|
| 2о | Если 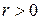 , то связь прямая, если , то связь прямая, если 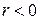 – связь обратная. – связь обратная.
|
| 3о | При 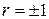 связь между связь между 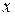 и и 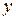 функциональная. функциональная.
|
| 4о | При 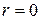 линейная связь между линейная связь между 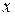 и и 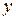 отсутствует. отсутствует.
|
Для оценки качества построенной модели регрессии можно использовать коэффициент детерминации 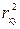 либо среднюю ошибку аппроксимации
либо среднюю ошибку аппроксимации 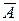 .
.
Коэффициент детерминации 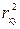 – квадрат коэффициента корреляции –показывает, какая часть вариации
– квадрат коэффициента корреляции –показывает, какая часть вариации 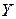 объясняется с помощью регрессии. Например, если
объясняется с помощью регрессии. Например, если  , то это означает, что на 90% переменная
, то это означает, что на 90% переменная 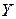 обусловлена переменной
обусловлена переменной 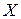 , т.е. объясняется моделью, а на 10% другими причинами.
, т.е. объясняется моделью, а на 10% другими причинами.
Коэффициент 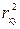 изменяется в пределах
изменяется в пределах 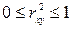 . Чем ближе
. Чем ближе 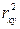 к 1, тем лучше уравнение регрессии, тем лучше модель описывает исходные данные.
к 1, тем лучше уравнение регрессии, тем лучше модель описывает исходные данные.
Средняя ошибка аппроксимации 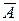 – среднее относительное отклонение расчетных значений от фактических
– среднее относительное отклонение расчетных значений от фактических
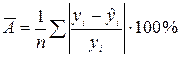
| (1.4) |
Построенное уравнение регрессии считается удовлетворительным, если значение 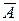 не превышает 10–12%.
не превышает 10–12%.
 2014-02-02
2014-02-02 478
478








