2014-02-02
348
1) 
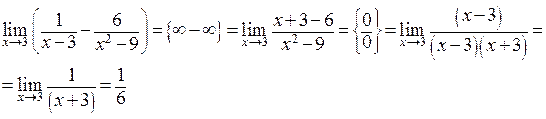
2) 
.
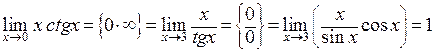3) Проверить непрерывность функции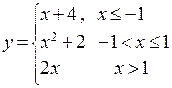 
.
Поскольку функци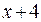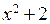и 
, 
и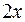 
непрерывны в областях их задания, достаточно рассмотреть функцию 
в точках стыковки этих функций. Итак, для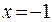 
имеем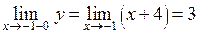 
, 
, 
.
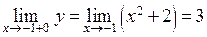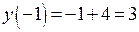Функция в этой точке непрерывна согласно определению 4.
Для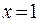 
имеем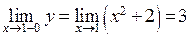 
, 
, 
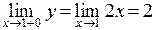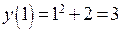. Условие непрерывности в точке 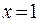не выполняется.
Следовательно, функция непрерывна на всей числовой оси за исключением точки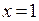 
, где она имеет конечный разрыв со скачком
(-1).
